Q:

Write a program to print Level Order Traversal in spiral form of a binary tree

mahmoud2506
Save to bookmark
|
2022-04-30
|
  362 
0

Level order traversal in spiral form

Write a program to print Level Order Traversal in spiral form of a binary tree.

Example:

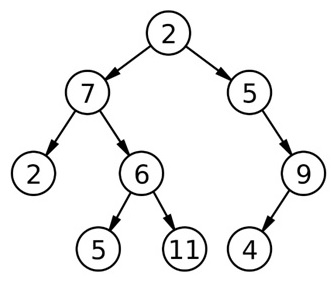
Level order traversal in spiral form

For the above tree:
Basic level order traversal:
    2
    7 5
    2 6 9
    5 11 4
Level order traversal in spiral form:
    2
    7 5 (left to right)
    9 6 2 (right to left)
    5 11 4 (again left to right)
C++ programming, Interview questions, C++ programming Interview-questions,
login and add your own answer to this question

All Answers

mahmoud2506
2022-04-30
need an explanation for this answer? contact us directly to get an explanation for this answer

The solution will, of course, surround basic level order traversal. The spiral order means - It will go from left to right for one level, then right to left for next level and again left to right for the next one and so on.

We need to modify our basic level order traversal.

We can do the flipping of direction (left → right then right → left so on ...) by keeping a flag variable which will be updated at end of each level.

Pre-requisite: Root to tree

1.  Declare flag as 1(true);
2.  Declare a queue q to store pointer to nodes(node*);
3.  Declare a stack s which helps us for flipping.
4.  Print the root as we are not going to bother about root level;
5.  IF(root->left) //left child exists
        ENQUEUE(q, root->left);
    END IF
    IF(root->right) //right child exists
        ENQUEUE(q, root->right);
    END IF
    IF root has no child
        RETURN BACK //nothing to print more
    ELSE
        q.push(NULL); //to indicate end of 1st level

6.  //Here goes the modified level order traversal
    When flag=1 its left-to right 
    flag=0 its right to left
    while (q is not empty){
        temp=DEQUEUE(q);	
        IF(temp==NULL) //end of last traversed level
            IF (q is not empty)
                ENQUEUE (q, NULL);
            END IF
            IF (flag==0)
                Pop and print data from stack until stack is empty
            END IF	
            flag=1-flag; //flip flag for next level 1 to 0 or 0 to 1
        ELSE
            IF(flag == 1)
                Print temp->data; //left to right printing		
            ELSE
                Push temp->data to stack s; //this makes right to left 
                //printing as rightmost node will be at the top of stack
            END IF-ELSE
            // basic level order traversal (direction left to right)
            IF(root->left) //left child exists
                ENQUEUE(q, root->left);
            END IF
            IF (root->right) //right child exists
                ENQUEUE(q, root->right);
            END IF
        END IF-ELSE (outer one)
    END WHILE loop
 

Example with Explanation:

    For the above tree root is being printed 
    
    first without any constraint
    2
    
    For the first level flag is 1
    
    Thus it prints immediately while accessing temp node
    7 5 (since basic traversal direction is always left to right)
    
    At the end of level flag flips to 0
    
    So while traversing instead of printing nodes at once, 
    nodes get stored in stack
    
    At the end of level all the nodes data being popped and printed.
    In stack
    9(top)
    6
    2

    Thus printing
    9 6 2 (right to left)
    
    Flag again flipped to 1
    
    Basic left to right printing
    5 11 4
    So the output is in spiral order

C++ implementation:

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class Node{
	public:
		int data;
		Node *left;
		Node *right;
};

// creating new node
Node* newnode(int data)  
{ 
	Node* node = (Node*)malloc(sizeof(Node)); 
	node->data = data; 
	node->left = NULL; 
	node->right = NULL; 
	return(node); 
} 

void printSpiral(Node *root)
{
	Node* temp;
	int flag=1;	
	queue<Node*> q;
	stack<int> s;
	
	cout<<root->data<<"\n";
	if(root->left)
		q.push(root->left);
	if(root->right)
		q.push(root->right);
	if(!root->left && !root->right)
		return;
	
	q.push(NULL);
	
	while(!q.empty()){
		temp=q.front();
		q.pop();
		if(temp==NULL){
			if(!q.empty())
				q.push(NULL);
			if(flag==0){
				while(!s.empty()){
					cout<<s.top()<<" ";
					s.pop();
				}
			}
			flag=1-flag;
			cout<<endl;
		}
		else{
			if(flag){
				cout<<temp->data<<" ";
			}
			else{
				s.push(temp->data);
			}
			if(temp->left)
				q.push(temp->left);
			if(temp->right)
				q.push(temp->right);
		}
	}
}


int main() { 
	//**same tree is builted as shown in example**
	Node *root=newnode(2); 
	root->left= newnode(7); 
	root->right= newnode(5); 
	root->right->right=newnode(9);
	root->right->right->left=newnode(4);
	root->left->left=newnode(2); 
	root->left->right=newnode(6);
	root->left->right->left=newnode(5);
	root->left->right->right=newnode(11);

	cout<<"Level Order traversal in spiral form of ";
	cout<<"the binary tree is :"<<endl; 
	printSpiral(root); 

	return 0; 
}

Output

 

Level Order traversal in spiral form of the binary tree is :
2
7 5
9 6 2
5 11 4

need an explanation for this answer? contact us directly to get an explanation for this answer

total answers (1)

Interview C++ coding problems/challenges | tree
This question belongs to these collections

Similar questions

need a help?

find thousands of online teachers now
Given a binary Tree find the maximum path sum. The... >>
<< Find the k-th smallest element in a given binary s...