Q:

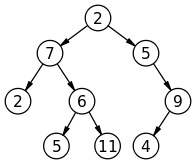
Given a Binary Tree write a program to print the nodes which don’t have a sibling node. Print all the nodes separated by space which do not have sibling in the tree in sorted order if every node has a tree than print -1

mahmoud2506
Save to bookmark
|
2022-04-30
|
  565 
0

Print All Nodes that don't have Sibling

Given a Binary Tree write a program to print the nodes which don’t have a sibling node. Print all the nodes separated by space which don't have sibling in the tree in sorted order if every node has a tree than print -1.

Tree 5

 

Explanation with example:

What is having sibling in tree?

A child node is said to have a sibling if the other node has the same parent as the child node. That means the nodes are siblings if they have same parent.

Like in the above example ‘2’ & ‘6’ are siblings as they have the same parent ‘7’.

In the above example the nodes that don’t have siblings are: 9, 4

Thus output:

4, 9 (sorted)

N.B: Root is not considered for sibling checking.

C++ programming, Interview questions, C++ programming Interview-questions,
login and add your own answer to this question

All Answers

mahmoud2506
2022-04-30
need an explanation for this answer? contact us directly to get an explanation for this answer

So, clearly a child node don’t have sibling, if its parent has only one pointer, either left or the right (that’s the child of course). Then we simply store the child node value & produce a sorted list to print. The traversal method we use here is level order traversal.

Algorithm:

1. Define tree Node structure
2. FUNCTION printSibling (Node* root)
    a) Declare a queue& a vector using STL 
    Queue<Node*>q;
    vector<int>store;
    b) push the root
    EnQueue(q,root);
    Node* temp;
    While(queue is not empty) //do the level order traversal & check for siblings
        temp=DeQueue(q);
        //if the current node has only one child, definitely the child 
        //has no sibling, thus store the child node value
        //left child pointer in NULL, right is not
        If temp->left==NULL&&temp->right!=NULL  
            Addtemp->right node value in store;
        END IF
        //right child pointer in NULL, left is not
        If temp->left!=NULL&&temp->right==NULL 
            Add temp->left node value in store;
        END IF
        // do level order traversing
        IF(temp->right)
        EnQueue(q, temp->right);
        IF(temp->left)
        EnQueue(q, temp->left);
    END WHILE
    c) If no node found without having sibling then vector size is zero then print -1
    d) Elsesort the vector to print sorted node value
END FUNCTION

C++ implementation to Print All Nodes that don't have Sibling

#include <bits/stdc++.h>
using namespace std;

// tree node is defined
class tree{    
	public:
		int data;
		tree *left;
		tree *right;
};

void printSibling(tree* root)
{
	//Declare queue using STL 
	queue<tree*> q;
	//enqueue the root
	q.push(root);
	vector<int> store;

	tree* temp;
	//do the level order traversal & check for siblings
	while(!q.empty()){
		//dequeue
		temp=q.front();
		q.pop();
		//if the current node has only one child 
		//definitely the child has no sibling
		//store the child node value
		if(temp->left==NULL && temp->right!=NULL){
			store.push_back(temp->right->data);
		}

		if(temp->left!=NULL && temp->right==NULL){
			store.push_back(temp->left->data);
		}
		// do level order traversing
		if(temp->right)
			q.push(temp->right);
		if(temp->left)
			q.push(temp->left);
	}
	//if no node found without having sibling
	//vector size is zero
	//print -1
	if(store.size()==0){
		printf("-1, no such  node\n");
	return;
	}
	//sort the vector to print sorted node value
	sort(store.begin(),store.end());
	//printing
	for(auto it=store.begin();it!=store.end();it++)
		printf("%d ",*it);
}

tree* newnode(int data)  // creating new node
{ 
	tree* node = (tree*)malloc(sizeof(tree)); 
	node->data = data; 
	node->left = NULL; 
	node->right = NULL; 

	return(node); 
} 


int main() 
{ 
	//**same tree is builted as shown in example**
	cout<<"same tree is built as shown in example\n";
	tree *root=newnode(2); 
	root->left= newnode(7); 
	root->right= newnode(5); 
	root->right->right=newnode(9);
	root->right->right->left=newnode(4);
	root->left->left=newnode(2); 
	root->left->right=newnode(6);
	root->left->right->left=newnode(5);
	root->left->right->right=newnode(11);

	cout<<"printing the nodes that don't have sibling...\n"<<endl; 
	printSibling(root);

	return 0; 
}

Output

same tree is built as shown in example
printing the nodes that don't have sibling...

4 9

need an explanation for this answer? contact us directly to get an explanation for this answer

total answers (1)

Interview C++ coding problems/challenges | tree
This question belongs to these collections

Similar questions

need a help?

find thousands of online teachers now
Given a Two Binary Trees, write a function that re... >>
<< Given a Binary Tree T and a sum S, write a program...