Q:

Given a Binary Tree and a target key, write a function that prints all the ancestors of the key in the given binary tree

mahmoud2506
Save to bookmark
|
2022-04-30
|
  371 
0

Ancestors in Binary Tree

Given a Binary Tree and a target key, write a function that prints all the ancestors of the key in the given binary tree.

Example:

Let's the tree be like following:

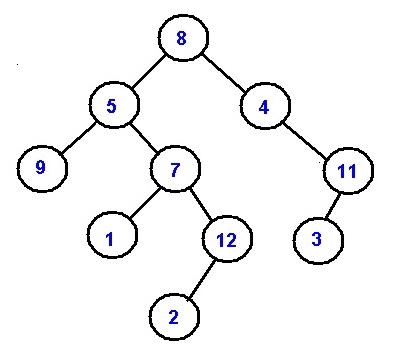
Ancestors in Binary Tree

    Let for node value 12:
    Ancestors are:
    7, 5, 8
    While for node value 7:
    Ancestors are:
    5, 8
C++ programming, Interview questions, C++ programming Interview-questions,
login and add your own answer to this question

All Answers

mahmoud2506
2022-04-30
need an explanation for this answer? contact us directly to get an explanation for this answer

What is Ancestors?

For any node n,
Its ancestors are the nodes which are on the path between roots to node n

Thus for the above examples,

Example 1:

    Node is 12 //represented by value
    Root to the node path is
    8->5->7->12
    Thus the ancestors are 7, 5, 8

Example 2:

    Node is 7 //represented by value
    Root to the node path is
    8->5->7
    Thus the ancestors are 5, 8

Algorithm:

FUNCTION printAncestors(Node *root, int target)
    IF(!root)
        return false;
    IF( (root->left && root->left->data==target) ||
        (root->right && root->right->data==target ) || 
        printAncestors(root->left,target)|| 
        printAncestors(root->right,target)){
            Print root->data;
            return true;
    END IF
    return false;
END FUNCTION

That simply means we are doing kind of DFS

For a currentnode to be ancestor of the target node the conditions are:

1.  If the target node is its child node (either left child or right child)
    //condition
    IF((root->left && root->left->data==target) ||
    (root->right && root->right->data==target ))

2.  If any of the two subtree of the current node contain ancestor of the target 
    node then the current node is also an ancestor. 
    //condition
    IF(printAncestors(root->left, target)|| 
    printAncestors(root->right, target))

Example with explanation:

For target node 7:
Root 8 is ancestor on condition: its left subtree contains ancestor 5
5 is ancestor since target node is its right child
Thus ancestors are:
5, 8 //in order

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

//tree node
class Node{ 
	public:
	int data;
	Node *left;
	Node *right;
};

bool printAncestors(Node *root, int target)
{
	if(!root)
	return false;

	if(	(root->left && root->left->data==target) ||
		(root->right && root->right->data==target ) || 
		printAncestors(root->left,target)|| 
		printAncestors(root->right,target)){
		cout<<root->data<<" ";
		return true;
	}
	return false;
}

//creating new nodes
Node* newnode(int data){  
	Node* node = (Node*)malloc(sizeof(Node)); 
	node->data = data; 
	node->left = NULL; 
	node->right = NULL; 
	return(node); 
} 

int main() { 
	//**same tree is builted as shown in example**
	cout<<"tree in the example is build here"<<endl;
	//building the tree like as in the example
	Node *root=newnode(8); 
	root->left= newnode(5); 
	root->right= newnode(4); 
	root->right->right=newnode(11);
	root->right->right->left=newnode(3);
	root->left->left=newnode(9); 
	root->left->right=newnode(7);
	root->left->right->left=newnode(1);
	root->left->right->right=newnode(12);
	root->left->right->right->left=newnode(2);

	int s;

	cout<<"enter input value to find ancestors......"<<endl;
	cin>>s;

	printAncestors(root,s);
	return 0; 
}

Output

 

tree in the example is build here
enter input value to find ancestors......
7
5 8

need an explanation for this answer? contact us directly to get an explanation for this answer

total answers (1)

Interview C++ coding problems/challenges | tree
This question belongs to these collections

Similar questions

need a help?

find thousands of online teachers now
Given a Binary Tree of size N, write a program tha... >>
<< Given a binary tree, print the bottom view from le...