Q:

Program to find the total number of possible Binary Search Trees with n keys

belongs to collection: Tree Programs

robaa
Save to bookmark
|
2022-11-09
|
  278 
0

Explanation

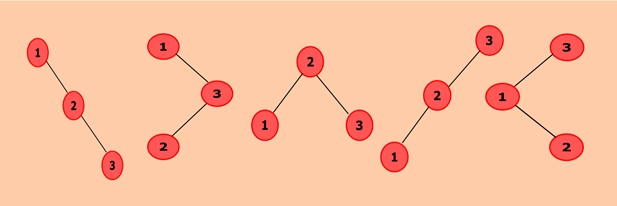
In this program, we need to find out the total number of binary search trees can be constructed with n values. Below diagram shows a possible binary search tree with the key value as 3. So, we can construct a total of five binary search trees. When we choose node 1 as the root node, we get two trees. Similarly, one tree with 2 as root node and two trees when we select 3 as the root node.

This approach involves selecting a node recursively as the root node and create possible binary search tree.

An easy way to calculate the total number of possible binary search trees are through Catalan number:

Cn = (2n)! / n! *(n+1)!  

Algorithm

  1. Define Node class which has three attributes namely: data left and right. Here, left represents the left child of the node and right represents the right child of the node.
  2. When a node is created, data will be passed to the data attribute of the node and both left and right will be set to null.
  3. Define another class which has an attribute root.
    1. Root represents the root node of the tree and initialize it to null.
  4. numOfBST() will find out total possible binary search tree for given key:
    1. It will calculate the Catalan number for given key by making a call to factorial().
    2. Catalan number can be calculated using the formula:
      Cn = (2n)! / n! *(n+1)!
    3. Factorial() will calculate factorial of a given number.

Output:

Total number of possible Binary Search Trees with given key: 42
Python programming, Php programming, Java programming, C programming, c# programming, examples, Python programming examples, Php programming examples, Java programming examples, C programming examples, c# programming examples,
login and add your own answer to this question

All Answers

robaa
2022-11-09
need an explanation for this answer? contact us directly to get an explanation for this answer

Python

#Represent a node of binary tree  
class Node:  
    def __init__(self,data):  
        #Assign data to the new node, set left and right children to None  
        self.data = data;  
        self.left = None;  
        self.right = None;  
   
class BinarySearchTree:  
    def __init__(self):  
        #Represent the root of binary tree  
        self.root = None;  
          
    #factorial() will calculate the factorial of given number  
    def factorial(self, num):  
        fact = 1;  
        if(num == 0):  
            return 1;  
        else:  
            while(num > 1):  
                fact = fact * num;  
                num = num - 1;  
            return fact;  
      
    #numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key  
    def numOfBST(self, key):  
        catalanNumber = self.factorial(2 * key)/(self.factorial(key + 1) * self.factorial(key));  
        return int(catalanNumber);  
   
bt = BinarySearchTree();  
   
#Display the total number of possible binary search tree with key 5  
print("Total number of possible Binary Search Trees with given key: " + str(bt.numOfBST(5)));

 

Output:

Total number of possible Binary Search Trees with given key: 42

 

C

#include <stdio.h>  
#include <stdlib.h>  
   
//Represent a node of binary tree  
struct node{  
    int data;  
    struct node *left;  
    struct node *right;  
};  
   
//Represent the root of binary tree  
struct node *root = NULL;  
   
//createNode() will create a new node  
struct node* createNode(int data){  
    //Create a new node  
    struct node *newNode = (struct node*)malloc(sizeof(struct node));  
    //Assign data to newNode, set left and right child to NULL  
    newNode->data = data;  
    newNode->left = NULL;  
    newNode->right = NULL;  
    return newNode;  
}  
   
//factorial() will calculate the factorial of given number  
int factorial(int num) {  
    int fact = 1;  
    if(num == 0)  
        return 1;  
    else {  
        while(num > 1) {  
            fact = fact * num;  
            num--;  
        }  
        return fact;  
    }  
}  
   
//numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key  
int numOfBST(int key) {  
    int catalanNumber = factorial(2 * key)/(factorial(key + 1) * factorial(key));  
    return catalanNumber;  
}  
      
int main(){  
      
    //Display total number of possible binary search tree with key 5  
    printf("Total number of possible Binary Search Trees with given key: %d", numOfBST(5));  
      
    return 0;  
}

 

Output:

Total number of possible Binary Search Trees with given key: 42

 

JAVA

public class BinarySearchTree {  
      
    //Represent the node of binary tree  
    public static class Node{  
        int data;  
        Node left;  
        Node right;  
          
        public Node(int data){  
            //Assign data to the new node, set left and right children to null  
            this.data = data;  
            this.left = null;  
            this.right = null;  
            }  
        }  
      
    //Represent the root of binary tree  
    public Node root;  
      
    public BinarySearchTree(){  
        root = null;  
    }  
      
    //factorial() will calculate the factorial of given number  
    public int factorial(int num) {  
        int fact = 1;  
        if(num == 0)  
            return 1;  
        else {  
            while(num > 1) {  
                fact = fact * num;  
                num--;  
            }  
            return fact;  
        }  
    }  
      
    //numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key  
    public int numOfBST(int key) {  
        int catalanNumber = factorial(2 * key)/(factorial(key + 1) * factorial(key));  
        return catalanNumber;  
    }  
      
    public static void main(String[] args) {  
          
        BinarySearchTree bt = new BinarySearchTree();  
          
        //Display total number of possible binary search tree with key 5  
        System.out.println("Total number of possible Binary Search Trees with given key: " + bt.numOfBST(5));  
      }  
}

 

Output:

Total number of possible Binary Search Trees with given key: 42

 

C#

using System;  
namespace Tree   
{                       
    public class Program  
    {  
        //Represent a node of binary tree  
        public class Node<T>{  
            public T data;  
            public Node<T> left;  
            public Node<T> right;  
              
            public Node(T data) {  
                //Assign data to the new node, set left and right children to null  
                this.data = data;  
                this.left = null;  
                this.right = null;  
            }  
        }  
          
        public class BinarySearchTree<T>{  
            //Represent the root of binary tree  
            public Node<T> root;  
   
            public BinarySearchTree(){  
                root = null;  
            }  
          
            //factorial() will calculate the factorial of given number  
            public int factorial(int num) {  
                int fact = 1;  
                if(num == 0)  
                    return 1;  
                else {  
                    while(num > 1) {  
                        fact = fact * num;  
                        num--;  
                    }  
                    return fact;  
                }  
            }  
   
            //numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key  
            public int numOfBST(int key) {  
                int catalanNumber = factorial(2 * key)/(factorial(key + 1) * factorial(key));  
                return catalanNumber;  
            }  
        }  
          
        public static void Main()  
        {  
            BinarySearchTree<int> bt = new BinarySearchTree<int>();  
          
            //Display total number of possible binary search tree with key 5  
            Console.WriteLine("Total number of possible Binary Search Trees with given key: " + bt.numOfBST(5));                  
        }      
    }

 

Output:

Total number of possible Binary Search Trees with given key: 42

 

PHP

<!DOCTYPE html>  
<html>  
<body>  
<?php  
//Represent a node of binary tree  
class Node{  
    public $data;  
    public $left;  
    public $right;  
      
    function __construct($data){  
        //Assign data to the new node, set left and right children to NULL  
        $this->data = $data;  
        $this->left = NULL;  
        $this->right = NULL;  
    }  
}  
class BinarySearchTree{  
    //Represent the root of binary tree  
    public $root;  
    function __construct(){  
        $this->root = NULL;  
    }  
      
    //factorial() will calculate the factorial of given number  
    function factorial($num) {  
        $fact = 1;  
        if($num == 0)  
            return 1;  
        else {  
            while($num > 1) {  
                $fact = $fact * $num;  
                $num--;  
            }  
            return $fact;  
        }  
    }  
      
    //numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key  
    function numOfBST($key) {  
        $catalanNumber = $this->factorial(2 * $key)/($this->factorial($key + 1) * $this->factorial($key));  
        return $catalanNumber;  
    }  
}  
   
$bt = new BinarySearchTree();  
          
//Display total number of possible binary search tree with key 5  
print "Total number of possible Binary Search Trees with given key: " . $bt->numOfBST(5);        
?>  
</body>  
</html>

 

Output:

Total number of possible Binary Search Trees with given key: 42

need an explanation for this answer? contact us directly to get an explanation for this answer

total answers (1)

Tree Programs
This question belongs to these collections

Similar questions

need a help?

find thousands of online teachers now
Program to implement Binary Tree using the linked ... >>
<< Program to find the sum of all the nodes of a Bina...