Q:

Program to display the upper triangular matrix

belongs to collection: Matrix Programs

robaa
Save to bookmark
|
2022-11-09
|
  170 
0

Explanation

In this program, we need to display the upper triangular matrix.

Upper Triangular Matrix

Upper triangular matrix is a square matrix in which all the elements below the principle diagonal are zero. To find the upper triangular matrix, a matrix needs to be a square matrix that is, the number of rows and columns in the matrix needs to be equal. Dimensions of a typical square matrix can be represented by n x n.

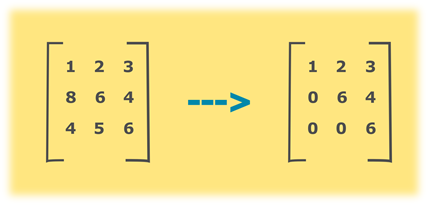
Consider the above example, principle diagonal element of given matrix is (1, 6, 6). All the elements below diagonal needs to be zero to convert it into an upper triangular matrix, in our example, those elements are at positions (2,1), (3,1) and (3,2). To convert given matrix into the upper triangular matrix, loop through the matrix and set the values of the element to zero where row number is greater than column number.

Algorithm

  1. Declare and initialize a two-dimensional array a.
  2. Calculate the number of rows and columns present in the array and store it in variables rows and cols respectively.
  3. If the number of rows is not equal to the number of columns, it implies that the given matrix is not a square matrix. Hence, given matrix cannot be converted to the upper triangular matrix. Display the error message.
  4. If rows = cols, traverse the array a using two loops where outer loop represents the rows, and inner loop represents the columns of the array a. To convert given matrix to upper triangular matrix set the elements of the array to 0 where (i > j) that is, the row number is greater than column number.
  5. Display the resulting matrix.

Input:

Matrix a = [1, 2, 3]  

           [8, 6, 4]  

           [4, 5, 6]  

Output:

Upper triangular matrix: [1 2 3]
                         [0 6 4]
                         [0 0 6]
Php programming, Python programming, Java programming, C programming, c# programming, examples, Php programming examples, Python programming examples, Java programming examples, C programming examples, c# programming examples,
login and add your own answer to this question

All Answers

robaa
2022-11-09
need an explanation for this answer? contact us directly to get an explanation for this answer

Python

#Initialize matrix a  
a = [     
       [1, 2, 3],  
       [8, 6, 4],  
       [4, 5, 6]  
    ];  
   
#Calculates number of rows and columns present in given matrix  
rows = len(a);  
cols = len(a[0]);  
   
if(rows != cols):  
    print("Matrix should be a square matrix");  
else:     
    #Performs required operation to convert given matrix into upper triangular matrix  
    print("Upper triangular matrix: ");  
    for i in range(0, rows):  
        for j in range(0, cols):  
            if(i > j):  
                print("0"),  
            else:  
                print(a[i][j]),  
   
        print(" ");

 

Output:

Upper triangular matrix: 
1 2 3 
0 6 4 
0 0 6

 

C

#include <stdio.h>  
   
int main()  
{  
    int rows, cols;  
          
    //Initialize matrix a  
    int a[][3] = {     
                    {1, 2, 3},  
                    {8, 6, 4},  
                    {4, 5, 6}  
                 };  
      
    //Calculates number of rows and columns present in given matrix  
    rows = (sizeof(a)/sizeof(a[0]));  
    cols = (sizeof(a)/sizeof(a[0][0]))/rows;  
      
    if(rows != cols){  
        printf("Matrix should be a square matrix\n");  
    }  
    else{  
        //Performs required operation to convert given matrix into upper triangular matrix  
        printf("Upper triangular matrix: \n");  
        for(int i = 0; i < rows; i++){  
            for(int j = 0; j < cols; j++){  
              if(i > j)  
                printf("0 ");  
              else  
                printf("%d ", a[i][j]);  
            }  
            printf("\n");  
        }  
    }  
          
    return 0;  
}

 

Output:

Upper triangular matrix: 
1 2 3 
0 6 4 
0 0 6

 

JAVA

public class UpperTriangular  
{  
    public static void main(String[] args) {  
        int rows, cols;  
          
        //Initialize matrix a  
        int a[][] = {     
                        {1, 2, 3},  
                        {8, 6, 4},  
                        {4, 5, 6}  
                    };  
            
          //Calculates number of rows and columns present in given matrix  
          rows = a.length;  
        cols = a[0].length;  
          
        if(rows != cols){  
            System.out.println("Matrix should be a square matrix");  
        }  
        else {  
            //Performs required operation to convert given matrix into upper triangular matrix  
            System.out.println("Upper triangular matrix: ");  
            for(int i = 0; i < rows; i++){  
                for(int j = 0; j < cols; j++){  
                  if(i > j)  
                    System.out.print("0 ");  
                  else  
                    System.out.print(a[i][j] + " ");  
                }  
                System.out.println();  
            }  
        }  
    }  
}

 

Output:

Upper triangular matrix: 
1 2 3 
0 6 4 
0 0 6

 

C#

using System;  
                      
public class UpperTriangular  
{  
    public static void Main()  
    {  
        int rows, cols;  
          
        //Initialize matrix a  
        int[,] a = {     
                        {1, 2, 3},  
                        {8, 6, 4},  
                        {4, 5, 6}  
                   };  
            
          //Calculates number of rows and columns present in given matrix  
          rows = a.GetLength(0);  
        cols = a.GetLength(1);  
          
        if(rows != cols){  
            Console.WriteLine("Matrix should be a square matrix");  
        }  
        else {  
            //Performs required operation to convert given matrix into upper triangular matrix  
            Console.WriteLine("Upper triangular matrix: ");  
            for(int i = 0; i < rows; i++){  
                for(int j = 0; j < cols; j++){  
                  if(i > j)  
                    Console.Write("0 ");  
                  else  
                    Console.Write(a[i,j] + " ");  
                }  
                Console.WriteLine();  
            }  
        }  
    }  
}

 

Output:

Upper triangular matrix: 
1 2 3 
0 6 4 
0 0 6

 

PHP

<!DOCTYPE html>  
<html>  
<body>  
<?php  
//Initialize matrix a  
$a = array(     
            array(1, 2, 3),  
            array(8, 6, 4),  
            array(4, 5, 6)  
          );  
   
//Calculates number of rows and columns present in given matrix  
$rows = count($a);  
$cols = count($a[0]);  
   
if($rows != $cols){  
    print("Matrix should be a square matrix<br>");  
}  
else {  
    //Performs required operation to convert given matrix into upper triangular matrix  
    print("Upper triangular matrix: <br>");  
    for($i = 0; $i < $rows; $i++){  
        for($j = 0; $j < $cols; $j++){  
          if($i > $j)  
            print("0 ");  
          else  
            print($a[$i][$j] . " ");  
        }  
        print("<br>");  
    }  
}  
?>  
</body>  
</html>

 

 

Output:

Upper triangular matrix: 
1 2 3 
0 6 4 
0 0 6

need an explanation for this answer? contact us directly to get an explanation for this answer

total answers (1)

Matrix Programs
This question belongs to these collections

Similar questions

need a help?

find thousands of online teachers now
Program to find the frequency of odd & even number... >>
<< Program to display the lower triangular matrix...