Let, there is N no. of values, say e1, e2, e3, ..., en and N is even.

    Subset1: { N/2  no. of values }
    Subset2: { N/2 no. of values }

The process to insert the elements to the Subsets is a problem of combination and permutation. To get the result we use the backtracking process. Here we take the sum of all the elements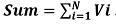 . Here we have to find out the elements that are in the subset no.1 and the elements that are not in subset1, must be in the subset no. 2. Every time we consider two things.

1. The ith element is a part of the subset1.
2. The ith element is not a part of the subset1.

After getting N/2 number of elements into the subset1. We will check,

If the value is less than then Difference we update the value of the Difference and make a note of the elements that are in the subset1.

After getting the elements for those the value of Difference is less we check the elements of the main set and find out the elements that are not in the subset1 and put them in subset2.

    Set: {1, 2, 3}
    Sum=6

1. 1 is in the subset1 therefore Subset1: {1} and Difference = abs(3-1) = 2
2. 2 is in the subset1 therefore Subset1: {1,2} and Difference = abs(3-3) = 0

Therefore, Difference is minimum.

    Subset1: {1,2}
    Subset2: {3}

C++ implementation:

#include <bits/stdc++.h>
using namespace std;

void traverse(int* arr, int i, int n, int no_of_selected, int sum, int& diff, bool* take, vector<int>& result, vector<int> current, int current_sum)
{
    //if the current position is greater than or equals to n
    if (i >= n)
        return;

    //if the value of difference is greater than
    //Sum/2-current sum of the elements of Subset no.1
    if ((diff > abs(sum / 2 - current_sum)) && (no_of_selected == (n + 1) / 2 || no_of_selected == (n - 1) / 2)) {
        diff = abs(sum / 2 - current_sum);
        //store the subset no. 1
        result = current;
    }

    //taking the elemets after the current element one by one
    for (int j = i; j < n; j++) {
        take[j] = true;
        current.push_back(arr[j]);
        traverse(arr, j + 1, n, no_of_selected + 1, sum, diff, take, result, current, current_sum + arr[j]);
        current.pop_back();
        take[j] = false;
    }
}

void find(int* arr, int n)
{
    //array to distinguished the elements those are in subset no. 1
    bool take[n];
    int sum = 0;

    for (int i = 0; i < n; i++) {
        sum += arr[i];
        take[i] = false;
    }

    int diff = INT_MAX;
    int no_of_selected = 0;

    vector<int> result;
    vector<int> current;

    int current_sum = 0;
    int i = 0;

    traverse(arr, i, n, no_of_selected, sum, diff, take, result, current, current_sum);

    set<int> s;

    //elements those are in subset no.1
    cout << "Set1 : { ";
    for (int j = 0; j < result.size(); j++) {
        cout << result[j] << " ";
        s.insert(result[j]);
    }
    cout << "}" << endl;

    //elements those are in subset no.2
    cout << "Set2 : { ";
    for (int j = 0; j < n; j++) {
        if (s.find(arr[j]) == s.end()) {
            cout << arr[j] << " ";
        }
    }
    cout << "}" << endl;
}

int main()
{
    int t;

    cout << "Test case : ";
    cin >> t;

    while (t--) {
        int n;
        cout << "Enter the value of n : ";
        cin >> n;
        int arr[n];
        cout << "Enter the values: ";
        //taking the set elements
        for (int i = 0; i < n; i++) {
            cin >> arr[i];
        }
        find(arr, n);
    }
    return 0;
}

Output

Test cases : 3
Enter the value of n : 3
Enter the values: 1 2 3
Set1 : { 1 2 }
Set2 : { 3 }
Enter the value of n : 4
Enter the values: 1 2 3 4
Set1 : { 2 3 }
Set2 : { 1 4 }
Enter the value of n : 10
Enter the values: 1 4 8 6 -7 -10 87 54 16 100
Set1 : { 4 -7 -10 87 54 }
Set2 : { 1 8 6 16 100 }