Adjacent are not allowed
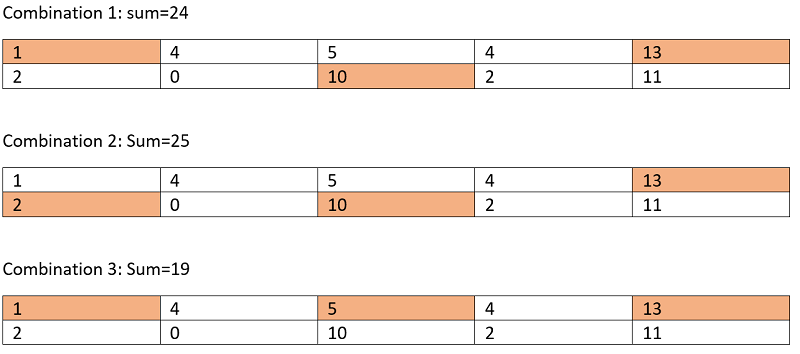
Given a rectangular grid of dimension 2 x N find out the maximum sum such that no two chosen numbers are adjacent, vertically, diagonally or horizontally.
Input:
The first line of input contains an integer T denoting the number of test cases.
The first line of each test case is N, number of columns in a grid, grid length.
Next two lines describes the 2*N grid.
Output:
Print the output for each test case in a separate line.
Constraints:
1 <= T<= 100 1 <= N<= 100 0 <= elements <= 100
Example:
Input: Test case: 1 Grid column size: 5 Grid as input: 1 4 5 4 13 2 0 10 2 11 Output: 25
Explanation:
The above grid is like following where many combinations are possible within the constraints.
Few have been shown below,
Since, we have got the maximum sum combination already, I am not considering the other combinations. The maximum sum possible to achieve is 25 which can be achieved from combination 2. (If you have doubt thinking about other combinations might produce better result, feel free to process other combinations too until you get exhausted)
So, the answer will be 25.
C++ programming
This is a standard recursion problem where we are supposed to either consider one number or not consider that number.
Say, the current element under our processing is: arr[r][c]
So, there are two choice,
If we formulate the recursive function, then it becomes,
f(r,c) = maximum(arr[r][c]+f(r,c-2),arr[r][c]+f(r-1,c-2), arr[r-1][c]+f(r,c-2),arr[r-1][c]+f(r-1,c-2), f(arr,r,c-1,n),f(r-1,c-1));The above recursion is generally illustrated on basis of assumption that all the indexed are valid.
The above recursion will generate many overlapping sub-problems and hence we need to memorize. Below is the detailed memorization process.
In the main function,
Initialize dp[3][n] with -1 which will store the computed sub-problem result.
Call the recursive function, myrecur(arr,0,0,n)
The function signature is described below,
Function myrecur(int arr[][],int r,int c,int n): if(r>=2) return 0; if(c>=n) return 0; // if already computed if(dp[r][c]!=-1) return dp[r][c]; // check for valid index if(r+1<2) dp[r][c] = maximum(arr[r][c] + myrecur(arr,r,c+2,n), arr[r][c] + myrecur(arr,r+1,c+2,n), arr[r+1][c] + myrecur(arr,r,c+2,n), arr[r+1][c] + myrecur(arr,r+1,c+2,n), myrecur(arr,r,c+1,n), myrecur(arr,r+1,c+1,n)); else dp[r][c] = maximum(arr[r][c] + myrecur(arr,r,c+2,n), arr[r][c] + myrecur(arr,r+1,c+2,n), myrecur(arr,r,c+1,n), myrecur(arr,r+1,c+1,n),INT_MIN,INT_MIN); end if else return dp[r][c] // which is the final maximum sum End functionC++ Implementation:
Output:
need an explanation for this answer? contact us directly to get an explanation for this answer