Longest Palindromic Substring
Given a string str, find the longest palindromic substring. A substring need to be consecutive such that for any xixj i<j must be valid in the parent string too. Like "incl" is a substring of "includehelp" while "iel" is not
Input:
The first line of input contains an integer T, denoting the no of test cases then T test cases follow. Each test case contains a tring str.
Output:
For each test case output will be a string which is the longest palindromic substring could be formed from the string str. There can be many valid answers, all are correct.
Constraints:
1 <= T <= 100
1 <= length of string str <= 300
Example:
Input:
test case:2
First test case:
Input string:
"aaaa"
Output:
Longest palindromic substring is: "aaaa"
Second test case:
Input string:
"abcaba"
Output:
Total count of palindromic sub-sequence is: "aba"
Explanation:
Test case 1: Input: "aaaa"
The valid palindromic substrings are shown below:
Marked cells are character taken in subsequence:
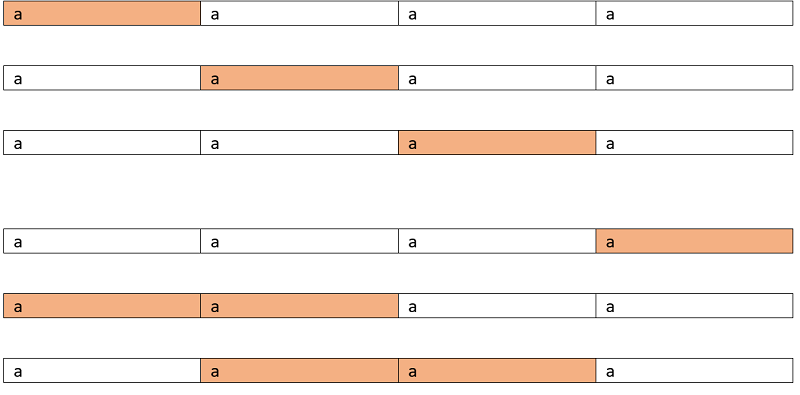

So the longest one is "aaaa"
For the second test case,
The substrings can be,
"a"
"b"
"c"
"aba"
So the longest one is "aba"






 C++ programming
C++ programming
This can be solved by using DP top-down approach,
Initially, p is the first character as that's the smallest palindrome of length 1 and max = 1.
Base case is that each single character is a palindrome itself. And for length of two, i.e, if adjacent characters are found to be equal then dp[i][i+1]=true, else if characters are different then dp[i][i+1]=false
To understand this lets think of a string like "acaa"
Here dp[0][1]=false
Whereas for dp[2][3] =true
So for higher lengths, if starting and ending index is the same then we recur for the remaining characters since we have the sub-problem result stored so we computed that. That's why we just update max to len as we are checking for increasing length at each iteration.
For proper understanding, you can compute the table by hand for the string "abcaba" to understand how it's working.
C++ Implementation:
Output:
need an explanation for this answer? contact us directly to get an explanation for this answer