Q:

Tower of Hanoi using recursion (C++ program)

mahmoud2506
Save to bookmark
|
2022-05-08
|
  599 
0

Obeying the following rules:

  1. Only one disk can be transfer at a time.
  2. Each move consists of taking the upper disk from one of the peg and placing it on the top of another peg i.e. a disk can only be moved if it is the uppermost disk of the peg.
  3. Never a larger disk is placed on a smaller disk during the transfer.

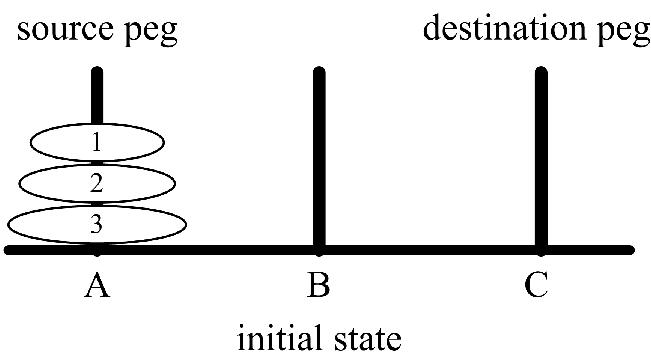
tower of HANOI implementation

(figure 1)

The solution to the puzzle calls for an application of recursive functions and recurrence relations.

A skeletal recursive procedure (Outline) for the solution of the problem for N number of disks is as follows:

  1. Move the top N-1 disks from peg A to peg B (using C as an auxiliarypeg)
  2. Move the bottom disk from peg A to peg C
  3. Move N-1 disks from Peg B to Peg C (using Peg A as an auxiliary peg)

The pictorial representation of the skeletal recursive procedure for N=4 disks is shown in Figure 2.

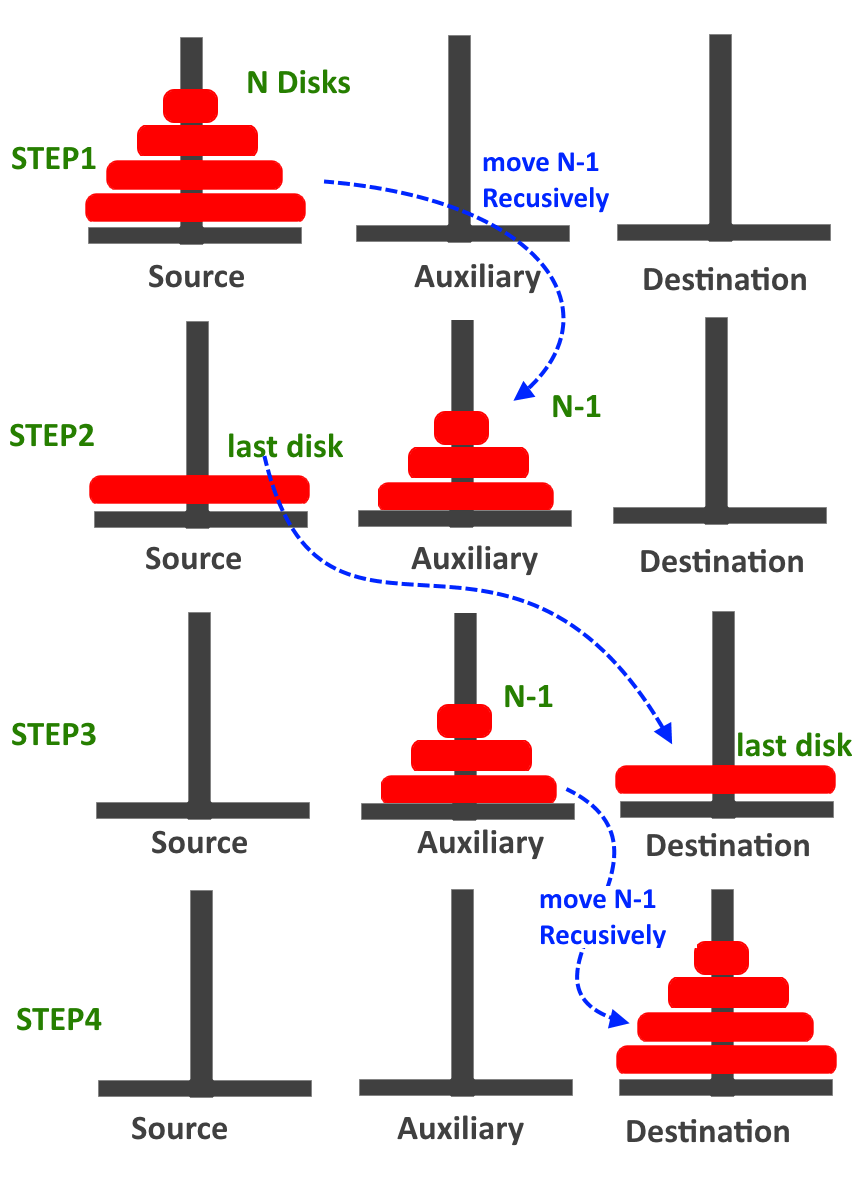
tower of HANOI implementation

 

C++ programming, exam questions, C++ programming exam-questions,
login and add your own answer to this question

All Answers

mahmoud2506
2022-05-08
need an explanation for this answer? contact us directly to get an explanation for this answer

Algorithm

TOH( n,  Sour, Aux , Des)
If(n=1)
    Write ("Move Disk “, n ," from ", Sour ," to ",Des)
Else
    TOH(n-1,Sour,Des,Aux);
    Write ("Move Disk “, n ," from ", Sour ," to ",Des)
    TOH(n-1,Aux,Sour,Des);
END

Let’s take an example to better understand the algorithm (For n=3).

tower of HANOI implementation

(figure 3)

Implementation of Tower of HANOI in using C++ program

#include<iostream>
using namespace std;

//tower of HANOI function implementation
void TOH(int n,char Sour, char Aux,char Des)
{ 
	if(n==1)
	{
		cout<<"Move Disk "<<n<<" from "<<Sour<<" to "<<Des<<endl;
		return;
	}
	
	TOH(n-1,Sour,Des,Aux);
	cout<<"Move Disk "<<n<<" from "<<Sour<<" to "<<Des<<endl;
	TOH(n-1,Aux,Sour,Des);
}

//main program
int main()
{ 
	int n;
	
	cout<<"Enter no. of disks:";	
	cin>>n;
	//calling the TOH 
	TOH(n,'A','B','C');
	
	return 0;
}

Output

Enter no. of disks:3
Move Disk 1 from A to C
Move Disk 2 from A to B
Move Disk 1 from C to B
Move Disk 3 from A to C
Move Disk 1 from B to A
Move Disk 2 from B to C
Move Disk 1 from A to C

 

need an explanation for this answer? contact us directly to get an explanation for this answer

total answers (1)

Data Structure programs using C and C++ (Sorting Programs)
This question belongs to these collections

Similar questions

need a help?

find thousands of online teachers now
Find in-order Successor and Predecessor in a BST u... >>
<< Maximum Sum Helix path (using C++ program)...