Count maximum points on same line
From a given set of input points find a maximum no of points on the same line.
Example:
Points are represented as a list of lists where the inner list is [x, y] representing a single point.
Input list:
[1,1] -> 1st point
[3,3] -> 2nd point
[-1,-1] -> 3rd point
[4, 4] -> 4th point
[5, 6] -> 5th point
[7,4] -> 6th point
The graph plotted is like below,
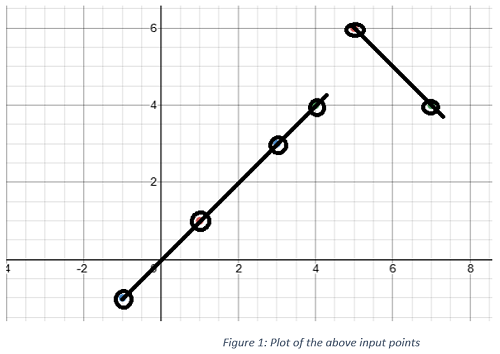
From the above input images, it’s visible that max no of point in the same line is 4. As there is 4 point in one line and the other line there are 2 points. So maximum points on the same line are 4.
Edge cases:
The edges cases for the problem is:
- In the inputs, there can be similar points which will be counted separately
To find whether three or more points are on the same line or not we need gradient (m) to check.
If two points are [x1,y1] and [x2,y2] then the gradient, m is calculated as: m=(y1-y2)/(x1-x2) or 1/m=(x1-x2)/(y1-y2)/
Now, m can be 0 when y1=y2 and can be infinity when x1=x2. While computing we need to take care of the infinity case as well.
So, the basic idea is, take two points as reference points for the line initially and check with other points how many points will fall on that line, i.e., will have the same gradient.
But this will take O(n^3) as we will require three loops to runs. Outer two loops will for two reference point selection and the inner one will be for other points selection.
Hashing can improve the complexity of keeping the logic the same. So what will be our hash function and how would we construct our hash table.
The idea is, we will have one point as reference and we will compute gradient with all the other points and store the gradient in our hash table and ill increment the same hash values.
So the hashing function, h(point)=gradient(x, reference point).
So it will have complexity only O(n^2) as the outer loop will be to choose the reference point and the inner loop to pick other points to compute the gradient. After completion of each inner loop, we will get the number of points falling in the same line with the reference point.
Finally, we will keep updating our maximum number of points after each outer loop iteration.
How to handle edge case of repeating points?
As mentioned earlier we may have the same points in the input list and both need to be considered separately. If we compute gradient we will find 0/0 which is indeterminate. So we need to keep a check for whether the other point is the same or not. If the same increment the count and finally add the count in max no of points for the reference point.
Check the detailed algorithm to understand fully and check the code to get the implementation.
Algorithm:
Input array of points=points 1. Set max_point=0 2. For each point o taking as reference point: Initialize an hash table to store the gradients Set temp_max_point =0 Set count=1 which will track same no of points for other points(edge case handling) For each other point p If p is not same as o Find gradient m b/w p and o Add gradient to the hash table like below mymap[m]++; update temp_max_point=max(temp_max_point,mymap[m]); else if p and o are same point increment count end if-else end for update max_point=max(max_point,count+ temp_max_point) (consider the same points too) end for max_point has the final resultC++ implementation:
Output:
need an explanation for this answer? contact us directly to get an explanation for this answer