The problem can be solved in a brute-force way. By generating all sub-sequences and checking them whether equal or not. Finally taking the longest common subsequence. But undoubtedly this is not at all computable since generating all sub-sequence is itself exponential and then permutations for checking any two sub-sequences.

The recursive way to solve is

Let,

        l1 = Length of the first string,str1
        l2 = Length of the second string,str2

f(l1,l2) = Longest common subsequence length for string lengths l1 & l2 

Now,

Think of the following example,

Say first string is: x1 x2 ... xl1

And the second string is: y1 y2 ... yl2

Say,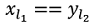 

Then obviously we need to find LCS for the remaining part of string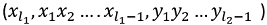  and then add 1 for this character match

Else

Maximum of two case

1. LCS of the first string leaving character  and second string 
2. LCS of the first string  and second string leaving character 

Now, we need to recur down to 0. So,

Where base cases are,

If you generate this recursion tree, it will generate many overlapping sub-problems and thus, we need to reduce the re-computing. That’s why we need to convert it into dynamic programming where we will store the output of the sub-problems and we will use it to compute bigger sub-problems.

Converting to Dynamic programing

    1)  Initialize dp[l1+1][l2+1]  to 0
    2)  Convert the base case of recursion:
            for i=0 to l1
                dp[i][0]=0;
            for i=0 to l2
                dp[0][i]=0;

    3)  Fill the DP table as per recursion.
        for i=1 to l1    //i be the subproblem length for str1
            for j=1 to l2 //j be the subproblem length for str2
                if(str1[i-1]==str2[j-1]) //xl1==yl2
                    dp[i][j]=dp[i-1][j-1]+1;
                else
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
            end for
        end for  
    4)  The final output will be dp[l1][l2]

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

int max(int a, int b)
{
    return (a > b) ? a : b;
}

int LCS(string str1, string str2)
{
    int l1 = str1.length();
    int l2 = str2.length();

    int dp[l1 + 1][l2 + 1];

    for (int i = 0; i <= l1; i++)
        dp[i][0] = 0;
    for (int i = 0; i <= l2; i++)
        dp[0][i] = 0;

    for (int i = 1; i <= l1; i++) {
        for (int j = 1; j <= l2; j++) {
            if (str1[i - 1] == str2[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
        }
    }

    return dp[l1][l2];
}
int main()
{
    string str1, str2;

    cout << "Enter first string\n";
    cin >> str1;
    cout << "Enter Second string\n";
    cin >> str2;

    cout << "Longest Common sub-sequence length is: " << LCS(str1, str2) << endl;

    return 0;
}

Output

Enter first string
includehelp
Enter Second string
letsincludeus
Longest Common sub-sequence length is: 7