Find the magic matrix
You are given a matrix of size N*N. You have to take another matrix of size N*N from which First you have to subtract the minimum value of each row from all the elements of the particular row and so on and after that operation, subtract the minimum value of each column from all the elements of that particular column. Then you have to check if the resulting matrix is matching the given matrix of size N*N.
Input
First line of the input is an integer N
Second line of the input is the matrix of size N*N
Output
Print "YES" if the resulting matrix is matching the given matrix.
Example:
Input:
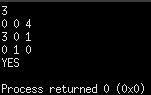
3
0 0 4
3 0 1
0 1 0
Output:
YES
Input:
3
3 1 5
0 5 3
2 0 5
Output:
NO
In input1, we can assume the matrix 3 1 5 7 2 3 5 4 3 In the first step: The smallest integer in row 1 is 1 The smallest integer in row 2 is 2 The smallest integer in row 3 is 3 After subtracting, the matrix becomes 2 0 4 5 0 1 2 1 0 And the second step is performed on this matrix. In the second step: The smallest integer in column 1 is 2 The smallest integer in column 2 is 0 The smallest integer in column 3 is 0 After subtracting, the resulting matrix is 0 0 4 3 0 1 0 1 0 And this is the matrix given on the input, so the answer is "YES". In Input2: We cannot assume any such matrix from which we can obtain the given matrix.Note: Before going to solution please try it by yourself.
Short description of solution approach
In this problem, whatever is talked about the second matrix from which you have to obtain the given matrix is just to puzzle you.
If you run behind the second matrix so there is a maximum probability that you are not going to get the correct answer for all input.
What you have to check is:
If these two conditions satisfy the matrix then your answer is YES otherwise NO.
Because the minimum value we can assume is 0. Now, if we subtract 0 from each row and each column of the matrix then we will be always getting the given matrix.
C++ implementation:
need an explanation for this answer? contact us directly to get an explanation for this answer