Where is my seat?
You and your friend are deciding to go for a tour by train. But before booking the ticket of the train, your friend asks you to book a ticket in such a way that both of you sit face to face.
Seating decoration is known to you (given in the image) and you as a VIP customer are allowed to book seat number according to your choice.
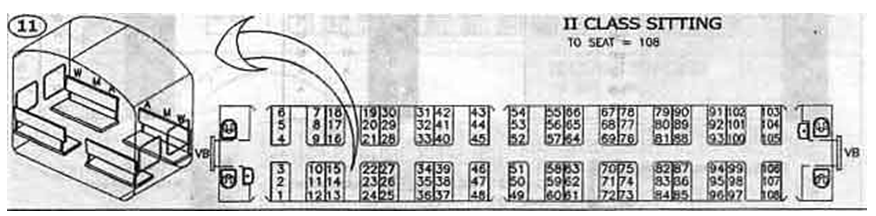
After booking the ticket accordingly, your friend asks you, your seat number so that he can check which is his seat number and seat position (WS/MS/AS)?
Example:
Input:
You have given your seat number N
Output:
Print your friend's seat number and seating position
WS: For Window Seat
MS: For Middle Seat
AS: For Aisle Seat
-----------------
Sample Input:
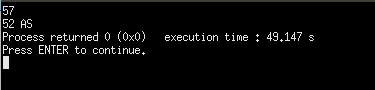
57
23
Sample Output:
52 AS
14 MS
Algorithm:
1. Take input N 2. Switch (N%12) 2.1 Case 1: print N+11 and "WS" 2.2 Case 2: print N+9 and "MS" 2.3 Case 3: print N+7 and "AS" 2.4 Case 4: print N+5 and "AS" 2.5 Case 5: print N+3 and "MS" 2.6 Case 6: print N+1 and "WS" 2.7 Case 7: print N-1 and "WS" 2.8 Case 8: print N-3 and "MS" 2.9 Case 9: print N-5 and "AS" 2.10 Case 10: print N-7 and "AS" 2.11 Case 11: print N-9 and "MS" 2.12 Default : print N-11 and "WS" 3. END OF PROGRAMExplanation:
Here we are finding mod of N (entered seat number) by 12 because there are 12 seats in a single cabin of the train. Now, if we divide it by 12 we will be able to identify each seat individually by its number, first 6 (1 to 6) are at the left side and next 6 (7 to 12) are at the right side.
For example, if N=52 then, N%12=4, so 52nd seat will get a unique number in that particular cabin and it is at the left side.
Now, by seeing the given picture we can say that difference between seat number 1 and 12 is 11, 2 and 11 is 9 and so on, means its decreasing by two, starting from 11.
So, for seat number 4 difference will be 5, that's why the opposite seat of 52 is 52+5=57.
Similarly, for N=23, the mod value is 11, and the seat difference of the opposite seat will be 9. But in this case, we have to deduct 9 from N because N is at the right side. So, ans: is 23-9=14.
C++ implementation:
Output

need an explanation for this answer? contact us directly to get an explanation for this answer