Largest Independent Set Problem
Given a tree, you have to find out the largest independent set. Independent elements are those that don’t have any common edges. Print the length of the largest independent set.
T Test case
T no. of input string will be given to you.
E.g.
2
 Output:
Print the length of the largest Independent set.
Output:
Print the length of the largest Independent set.
Example
T=2
Input:
 Output:
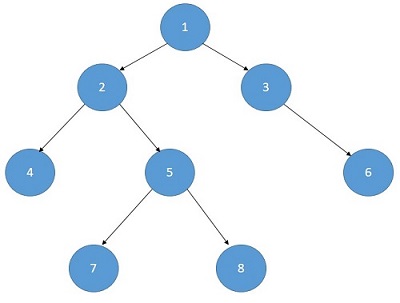
5 ( 1,4,7,8,6)
Input:
Output:
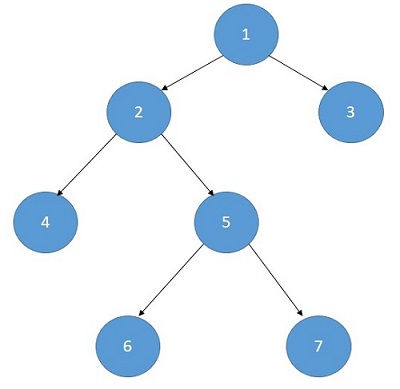
5 ( 1,4,7,8,6)
Input:
 Output:
4 (3,2,6,7)
Output:
4 (3,2,6,7)
Explanation with example:
To find out the length of the independent set we have to consider every node in our consideration.
- A node with its grandchildren are in the set
- The child nodes are in the set.
Independent set of node(x) = max (1+independent set of its grandchildren,independent set of its children)
Example:
 In that case,
Independent set of the node(1) =
max ( independent set of node(4), node(5) and node(6)+1 ,
independent set of the node(2)and node(3)
In that case,
Independent set of the node(1) =
max ( independent set of node(4), node(5) and node(6)+1 ,
independent set of the node(2)and node(3)
Recursive algorithm:
Function(Node): if(node==NULL) return 0 excluding_the_node=Function(node->left)+Function(node->right) including_the_node=1 if(node->left) including_the_node+=Function(node->left->left)+Function(node->left->right) if(node->right) including_the_node+=Function(node->right->left)+Function(node->right->right) return max(including_the_node,excluding_the_node)DP conversion:
Function(Node): if(node==NULL) return 0 if(vis[node]) return vis[node] excluding_the_node=Function(node->left)+Function(node->right) including_the_node=1 if(node->left) including_the_node+=Function(node->left->left)+Function(node->left->right) if(node->right) including_the_node+=Function(node->right->left)+Function(node->right->right) return vis[node]=max(including_the_node,excluding_the_node)C++ Implementation:
Output
need an explanation for this answer? contact us directly to get an explanation for this answer