Q:

Given a string str, find total number of possible palindromic sub-sequences. A sub-sequence does not need to be consecutive, but for any xixj i<j must be valid in the parent string too

mahmoud2506
Save to bookmark
|
2022-05-01
|
  333 
0

Count total number of Palindromic Subsequences

Given a string str, find total number of possible palindromic sub-sequences. A sub-sequence does not need to be consecutive, but for any xixj i<j must be valid in the parent string too. Like "icl" is a subsequence of "includehelp" while "ple" is not.

Input:

The first line of input contains an integer T, denoting the no of test cases then T test cases follow. Each test case contains a string str.

Output:

For each test case output will be an integer denoting the total count of palindromic subsequence which could be formed from the string str.

Constraints:

1 <= T <= 100
1 <= length of string str <= 300

Example:

Input:
Test case: 2

First test case:
Input string:
"aaaa"

Output:
Total count of palindromic subsequences is: 15

Second test case:
Input string:
"abaaba"

Output:
Total count of palindromic subsequences is: 31

Explanation:

Test case 1:

Input: "aaaa"

The valid palindromic subsequences are shown below,

Marked cells are character taken in subsequence:

Count=1

Count total number of Palindromic Subsequences (1)

Count=2

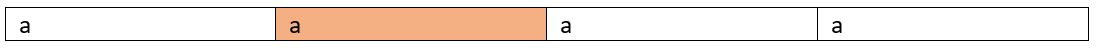
Count total number of Palindromic Subsequences (2)

Count=3

Count total number of Palindromic Subsequences (3)

Count=4

Count total number of Palindromic Subsequences (4)

Count=5

Count total number of Palindromic Subsequences (5)

Count=6

Count total number of Palindromic Subsequences (6)

Count=7

Count total number of Palindromic Subsequences (7)

Count=8

Count total number of Palindromic Subsequences (8)

Count=9

Count total number of Palindromic Subsequences (9)

Count=10

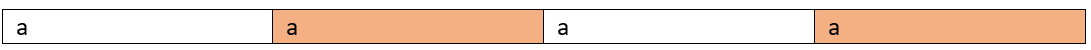
Count total number of Palindromic Subsequences (10)

Count=11

So on...
Total 15 palindromic sub-sequences
Actually in this case since all the character is same each and every subsequence is palindrome here.
For the second test case
Few sub-sequences can be
"a"
"b"
"a"
"aba"
So on
Total 31 such palindromic subsequences

C++ programming, Interview questions, C++ programming Interview-questions,
login and add your own answer to this question

All Answers

mahmoud2506
2022-05-01
need an explanation for this answer? contact us directly to get an explanation for this answer

This can be solved by using DP bottom up approach,

  1. Initialize dp[n][n] where n be the string length to 0
  2. Fill up the base case, Base case is that each single character is a palindrome itself. And for length of two, i.e, if adjacent characters are found to be equal then dp[i][i+1]=3, else if characters are different then dp[i][i+1]=2
    To understand this lets think of a string like "acaa"
    Here dp[0][1]=2 because there's only two palindrome possible because of "a" and "c".
    Whereas for dp[2][3] value will be 3 as possible subsequences are "a", "a", "aa". 
    for i=0 to n
    // for single length characters
    dp[i][i]=1; 
    if(i==n-1)
        break;        
    if(s[i]==s[i+1])
        dp[i][i+1]=3;
    else
        dp[i][i+1]=2;
end for
  3. Compute for higher lengths, 
    for len=3 to n
    for start=0 to n-len
        int end=start+len-1;
        // start and end is matching
        if(s[end]==s[start])
            // 1+subsequence from semaining part
            dp[start][end]=1+dp[start+1][end]+dp[start][end-1];
        else
            dp[start][end]=dp[start+1][end]+dp[start][end-1]-dp[start+1][end-1];
        end if
    end for
end for
  4. Final result is stored in dp[0][n-1];

So for higher lengths if starting and ending index is the same then we recur for the remaining characters, since we have the sub-problem result stored so we computed that. In case start and end index character are different then we have added dp[start+1][end] and dp[start][end-1] that's similar to recur for leaving starting index and recur for leaving end index. But it would compute dp[start+1][end-1] twice and that why we have deducted that.

For proper understanding you can compute the table by hand for the string "aaaa" to understand how it's working.

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

int countPS(string s)
{

    int n = s.length();
    int dp[n][n];
    
    memset(dp, 0, sizeof(dp));

    for (int i = 0; i < n; i++) {
        dp[i][i] = 1;
        if (i == n - 1)
            break;

        if (s[i] == s[i + 1])
            dp[i][i + 1] = 3;
        else
            dp[i][i + 1] = 2;
    }

    for (int len = 3; len <= n; len++) {
        for (int start = 0; start <= n - len; start++) {
            int end = start + len - 1;
            if (s[end] == s[start]) {
                dp[start][end] = 1 + dp[start + 1][end] + dp[start][end - 1];
            }
            else {
                dp[start][end] = dp[start + 1][end] + dp[start][end - 1] - dp[start + 1][end - 1];
            }
        }
    }

    return dp[0][n - 1];
}

int main()
{
    int t;
    cout << "Enter number of testcases\n";
    cin >> t;
    
    while (t--) {
        string str;
        cout << "Enter the input string\n";
        cin >> str;
    
        cout << "Total Number of palindromic Subsequences are: " << countPS(str) << endl;
    }
    
    return 0;
}

Output:

Enter number of testcases
2
Enter the input string
aaaa
Total Number of palindromic Subsequences are: 15
Enter the input string
abaaba
Total Number of palindromic Subsequences are: 31

need an explanation for this answer? contact us directly to get an explanation for this answer

total answers (1)

This question belongs to these collections

Similar questions

need a help?

find thousands of online teachers now