Shortest Common Super Sequence

Given two strings, you have to find the shortest common super sequence between them and print the length of the super sequence.

    Input:
    T Test case
    T no of input string will be given to you.

    E.g.
    3
    
    abcd abxy
    sghk rfgh
    svd vjhfd
    
    Constrain 
    1≤ length (string1) ≤100
    1≤ length (string2) ≤100
    
    Output:
    Print the length of the shortest super sequence formed from these two strings.

Example

    T=3

    Input:
    abcd abxy
    
    Output:
    6 (abcdxy)
    
    Input:
    sghk rfgh
    
    Output:
    6 (srfghk)
    
    Input:
    svd vjhfd
    
    Output:
    6 (svjhfd)

Explanation with example:

Let there are two strings str1 and str2.

    str1 = "abcd" 
    str2 = "abxy"

To find out the length of the super sequence from these two string is a bit difficult. To solve this problem we have to follow these steps:

We have to find out the longest common subsequence between the two strings. From "abcd" and "abxy" the longest common subsequence is "ab".
After getting the longest common subsequence we will add the non-common elements with the longest common subsequence. Non-common characters from "abcd" is "cd" and from "abxy" is "xy".
Therefore the length of the shortest common super sequence is:
```
    length of the two strings-length of the longest common subsequencs
```
The length of the shortest common super sequence is 6 (abcdxy)

Using a dynamic programming algorithm to find out the longest common subsequence between two given string is very efficient and fast as compared to the recursion approach.

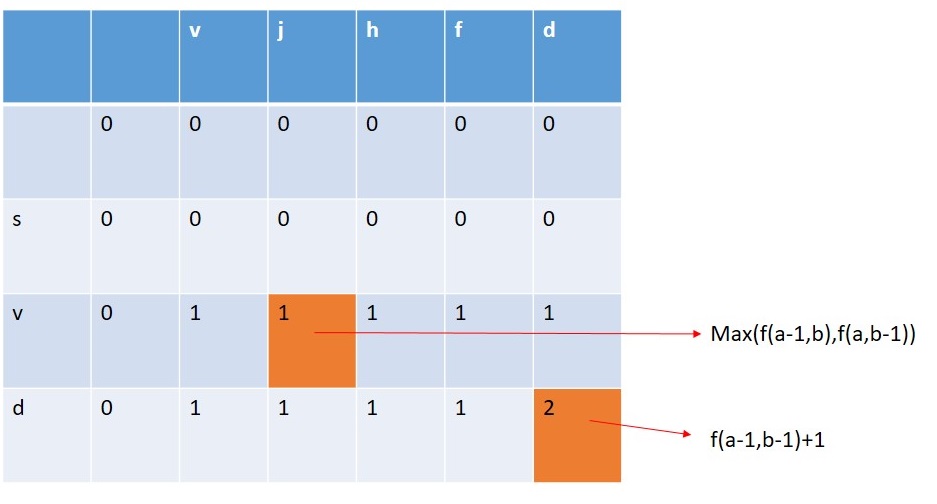
Let f(a,b) = count the number of common subsequences from the two string starting from 0 to position a and starting from 0 to position b.

Considering the two facts:

If the character of string1 at index a and character of string1 at index b are the same then we have to count how many characters are the same between the two strings before these indexes? Therefore,
```
    f(a,b)=f(a-1,b-1)+1
```
If the character of string1 at index a and character of string1 at index b are not same then we have to calculate the maximum common character count between (0 to a-1 of string1 and 0 to b of string2) and (0 to a of string1 and 0 to b-1 of string2).
```
    f(a,b)=max⁡(⁡(f(a-1,b),f(a,b-1))
```

For the two strings:

    str1 = "abcd"
    str2 = "abxy"

int Function(str1,pos1,str2,pos2): if pos1>=str1.length() || pos2>=str2.length() return 0 for a=pos1 to 0 for b=pos1 to 0 if str[a]==str[a+l-1] return Function(str1,a-1,str2,b-1)+1 else return max(Function(str1,a,str2,b-1),Function(str1,a-1,str2,b));

int Function(str1,str2): arr[len1+1][len2+1] for len=1 to str1.length() for a=1 to str2.length() if str[a]==str[b] arr[a][b]=arr[a-1][b-1]+1 else arr[a][b]=max(arr[a][b-1],arr[a-1][b]) return arr[len1-1][len2-1]

#include <bits/stdc++.h> using namespace std; int count_common_subsequence(string str1, string str2) { int len1 = str1.length(); int len2 = str2.length(); int arr[len1 + 1][len2 + 1]; memset(arr, 0, sizeof(arr)); for (int i = 1; i <= len1; i++) { for (int j = 1; j <= len2; j++) { if (str1[i - 1] == str2[j - 1]) { arr[i][j] = arr[i - 1][j - 1] + 1; } else { arr[i][j] = max(arr[i - 1][j], arr[i][j - 1]); } } } return arr[len1][len2]; } int main() { int t; cout << "Test Case : "; cin >> t; while (t--) { string str1, str2; cout << "Enter the strings : "; cin >> str1 >> str2; cout << "Length of the longest common subsequence: " << count_common_subsequence(str1, str2) << endl; } return 0; }

Test Case : 3 Enter the strings : svd vjhfd Length of the longest common subsequence: 2 Enter the strings : sghk rfgh Length of the longest common subsequence: 2 Enter the strings : abcd abxy Length of the longest common subsequence: 2

Given two strings, you have to find the shortest common super sequence between them and print the length of the super sequence

Shortest Common Super Sequence

All Answers

This question belongs to these collections

Similar questions

need a help?

find thousands of online teachers now