Longest Common Subsequence
Given two strings str1 and str2, find length of the longest common sub-sequence between them
Let the strings be
str1="includehelp"
str2="letsinclude"
Output will be:
Longest common sub-sequence length is 7
The longest common sub-sequence is: "include"

The output is given above where the longest common sub-sequences is in same colour.
The problem can be solved in a brute-force way. By generating all sub-sequences and checking them whether equal or not. Finally taking the longest common subsequence. But undoubtedly this is not at all computable since generating all sub-sequence is itself exponential and then permutations for checking any two sub-sequences.
The recursive way to solve is
Let,
Now,
Think of the following example,
Say first string is: x1 x2 ... xl1
And the second string is: y1 y2 ... yl2
Say,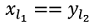
Then obviously we need to find LCS for the remaining part of string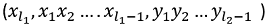 and then add 1 for this character match
and then add 1 for this character match
Else
Maximum of two case
Now, we need to recur down to 0. So,
Where base cases are,
If you generate this recursion tree, it will generate many overlapping sub-problems and thus, we need to reduce the re-computing. That’s why we need to convert it into dynamic programming where we will store the output of the sub-problems and we will use it to compute bigger sub-problems.
Converting to Dynamic programing
C++ Implementation:
Output
need an explanation for this answer? contact us directly to get an explanation for this answer