Maximum Sum Problem
Given a number n, we can divide it into only three parts n/2, n/3 and n/4 (we will consider only integer part). The task is to find the maximum sum we can make by dividing the number into three parts recursively and summing up them together.
Note: Sometimes, the maximum sum can be obtained by not dividing n.
Input:
The first line of input contains an integer T denoting the number of test cases.
Then T test cases follow. The first line of each test case contains the integer n.
Output:
For each test case, in a new line, print the maximum sum possible.
Example:
Input:
2
12
24
Output:
13
27
Explanation:
Say for the first example,
N=12
N can be divided in n/2(6), n/3(4) & n/4(3).
6 can be divided as 3, 2, 1.
3 can be divided as 1, 1, 0
So if n=3 then max sum possible is 3 itself
2 can be divided as 1, 0, 0
So if n=2 then max sum possible is 2 itself
1 can't be divided so, if n=1 then max sum possible is 1 itself
So, for n=6 max sum possible is either 6 or 3+2+1 whichever maximum, and its 6
Similarly for n=4 max sum possible is 4 (do it yourself)
For n=3, max sum possible is 3 (already found while computing for 6)
So for n=12
Max sum possible is either 12 or (max sum (6) + max sum (4) + max sum (3) = 13),
so it's 13
Check the following tree for proper understanding.
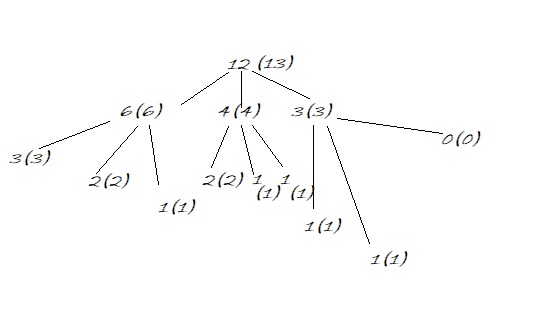
Try the second example of n=24 yourself.





 C++ programming
C++ programming
Obviously, this is recursion. The recursive algorithm can be,
Function axsum: 1) Base case: if n is 0 or n is 1 return n; 2) Return maximum( n,maxsum(n/2) + maxsum(n/3)+maxsum(n/4))This is the same as what I did in the above explanation. Compute until you reach the base case. But, the recursive solution will generate many overlapping subproblems which will be computed again and again. Check the above recursion tree for n=12, and you can find there have been multiple instances of subproblem 3 & 2 which are to be computed multiple times. If such small input generates these many overlapping subproblems then for large input it will be computationally very expensive. So, to overcome this overhead, we use dynamic programming which is storing the computed subproblems and use it whenever required again without further computing. This will reduce the overhead.
To store the computations we use dp an array with dimension equal to input size n
So,
1) Initialize dp[n+1] with the index value. That is, dp[0]=0,dp[1]=1 ,dp[2] =2 and so on. This covers to thing. i) It covers base case that is for n=0 or 1 ii) It initializes each sub problem of size i with value i which is the least value of the maximum sum. If maximum sum can't be availed by dividing then it will return i,sub problem size 2) for i=2 to n dp[i]=maximum(dp[i],dp[i/2]+dp[i/3]+dp[i/4]) 3) Return dp[n]This has time complexity of O(n) and space complexity of O(n).
N.B: To bring more optimization on multiple test cases, create a global array and pre-compute it. The global array should be based on input constraints. Check the following implementation.
C++ Implementation:
Output
need an explanation for this answer? contact us directly to get an explanation for this answer