Highway billboard
Consider a highway of M miles. The task is to place billboards on the highway such that revenue is maximized. The possible sites for billboards are given by number x1 < x2 < ... < x(n-1) < xn specifying positions in miles measured from one end of the road. If we place a billboard at position xi, we receive a revenue of ri > 0. The constraint is that no two billboards can be placed within t miles or less than it.
Input:
M=15, n=5
x[n]= {6,8,12,14,15}
revenue[n] = {3,6,5,3,5}
t = 5
Output:
11
Explanation with example
So, we have to maximize the revenue by placing the billboards where the gap between any two billboard is t.
Here,
The corresponding distances of the billboards with respect to the origin are,
x[5]= {6,8,12,14,15}
We can augment the origin, so the augmented array becomes: (no need to augment if origin revenue exists)
x[6]= {0,6,8,12,14,15}
t=5
The graphical interpretation of the billboards is like following:
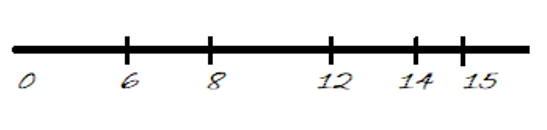
Figure 1: Billboards
The augmented revenue array:
revenue[6] = {0,3,6,5,3,5}
Now, the brute force approach can be to check all the possible combination of billboards and updating the maximum revenue accumulated from each possible combinations.
Few of such possible combinations can be:
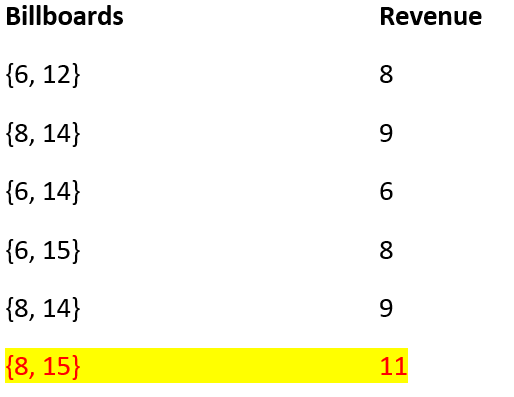
So, maximum revenue that can be collected is 11.
For any billboard bi we have three choices
- Don't pick bi
- Start from bi
- Pick bi and other billboards accordingly
Say,
M(i)=maximum revenue upto first i billboards
So,
M(0)=0
if bi is not picked, M(i)=M(i-1)
if billboard placement starts from bi M(i)=r[i]
If we place bi then need to pace bj where d[i]>d[j]-t such that revenue maximizes
So,
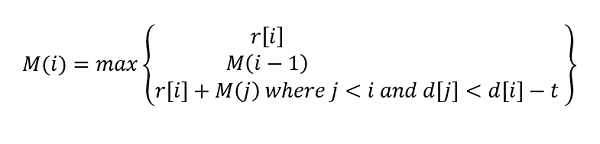
We convert the above recursion to dynamic programing as there will many overlapping sub problems solving the recursion. (Try to generate the recursion tree yourself)
1) Construct DP[n] for n billboards // considering billboard placing starts from it 2) Fill the array with base value which is r[i] 3) for i=1 to n-1 // recursion case 1 and 2 // either not picking ith billboard or starting // from ith billboard which ever is maximum dp[i] = max(dp[i-1],dp[i]); // recursion case 3 // picking ith billboard for j=0 to i-1 if(a[j]< a[i]-k)//feasible placing dp[i]= max(dp[i],dp[j]+r[i]); end for end for Result is dp[n-1]C++ implementation:
Output
need an explanation for this answer? contact us directly to get an explanation for this answer