Q:

You are given an array A of size N. The array contains integers and is of even length. The elements of the array represent N coin of values x1, x2, ... ,xn

mahmoud2506
Save to bookmark
|
2022-04-30
|
  122 
0

Optimal Strategy for a Game

You are given an array A of size N. The array contains integers and is of even length. The elements of the array represent N coin of values x1, x2, ... ,xn. The rule of game is:

  1. Each of the players gets alternative turns.
  2. In each turn, a player selects either the first or last coin from the row, removes it
  3. permanently, and receives the value of the coin.
  4. Both the player plays in an optimal way, i.e., both want to maximize total winning money.

You need to determine the maximum possible amount of money you can win if you start the game.

    Input
    N=4
    Array values:
    10 30 5 8

    Output:
    38

Example:

    Number of coins: 4
    Coin values:
    10 30 5 8

    To achieve maximum money:
    I will pick up 8 first (Not 10. Think Why?)
    So the row will be:
    10 30 5
    The opponent will pick 10 as that's optimal
    So the row will be:
    30 5
    I will pick 30
    Opponent will get 5

    Total my winnings: 8+30=38
    Total opponents winning: 10+5=15

Explanation:

The first thing that comes to our mind that we should go for the greedy method. Since we can only pick either first element or last element, let's pick the local best one, i.e., Pick the one which is maximum of first and last element. Let's see whether such a method would be optimal or not.

Let's take the same example,

    Coin values:
    10 30 5 8

    To achieve maximum money using greedy approach:
    I will pick up 10 first (maximum of 10 and 8)
    So the row will be:
    30 5 8
    The opponent will pick 30 as that's maximum of 30 and 8
    So the row will be:
    5 8
    I will pick 8
    Opponent will get 5

    Total my winnings: 10+8=18
    Total opponents winning: 30+5=35

Is this optimal? I got less money than the opponent. So we can simply choose the local best one ( Answer of Why), we can't go for greedy.

Let's check what can be optimal strategy,

Say the coins are,

    x1, x2, ..., xi, x(i+1), ..., x(j-1), x(j), ..., xn

Let,

    f(i,j)=maximum wiining for me when ith to jth coins are remaining

There at any stage of game
And it's my turn
So, I can either pick xi or xj based on the optimal choice.

  1. So If I choose xi , opponent will pick either of x(i+1) or xj leaving me with minimum(f(i+2,j),f(i+1,j-1)) 
        
    Opponent choosing x(i+1) corresponds to f(i+2,j)
    Opponent choosing xj corresponds to f(i+1,j-1)
  2. If I choose xj , opponent will pick either of xi or x(j-1) leaving me with minimum(f(i+1,j-1),f(i,j-2)) 
        Opponent choosing xi corresponds to f(i+1,j-1)
    Opponent choosing x(j-1) corresponds to f(i,j-2)

So, I will choose xi or xj what gives me maximum.
so,

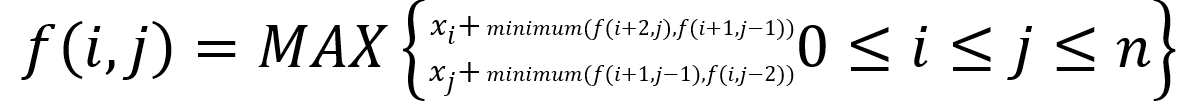
optimal strategy for a game step 1

Above is the recursion and we need to convert it into Dynamic Programming.

C++ programming, Interview questions, C++ programming Interview-questions,
login and add your own answer to this question

All Answers

mahmoud2506
2022-04-30
need an explanation for this answer? contact us directly to get an explanation for this answer

We need a 2D array to store f(i,j)

Say, DP[n][n] and the result will be DP[0][n-1] //maximum winning for coin 0th to nth (all the coins)

Base case:

    If there is only one coin left, there's no choice
        f(i,i)=arr[i] // arr is the array storing coin values in the row
    So,
    for i=0 to n-1
        DP[i][i]=arr[i]   
    END for

    If there is only two coin, i.e., xi, x(i+1)
    I will choose the maximum obviously for maximum winning
    for i=0 to n-2
        DP[i][i+1]=arr[i]   
    END for

To fill rest of the Table using the recursion,

    for (int len = 2; len < n; len++) {
        for (int i = 0, j = len; j < n; i++, j++) {
            DP[i][j] = max⁡(a[i] + min⁡(DP[i + 2][j], DP[i + 1][j - 1]),
                a[j] + min(DP[i + 1][j - 1], DP[i][j - 2]));
        }
    }

Initial DP table after computing base cases

DP[4][4] // N=4

optimal strategy for a game step 2

Filling up the upper triangular matrix

Len=2

optimal strategy for a game step 3

Len=3

optimal strategy for a game step 4

C++ implementation:

#include <bits/stdc++.h>
using namespace std;

int max(int x, int y)
{
    if (x > y)
        return x;
    else
        return y;
}
int min(int x, int y)
{
    if (x < y)
        return x;
    else
        return y;
}
int MAX_WINNING(vector<int> a, int n)
{

    int DP[n][n]; //DP matrix
    memset(DP, 0, sizeof(DP));
    //base case
    for (int i = 0; i < n; i++) {
        DP[i][i] = a[i];
        if (i != n - 1) {
            DP[i][i + 1] = (a[i] > a[i + 1]) ? a[i] : a[i + 1];
        }
    }
    //filling up table using recusrion
    for (int len = 2; len < n; len++) {
        for (int i = 0, j = len; j < n; i++, j++) {
            DP[i][j] = max(a[i] + min(DP[i + 2][j], DP[i + 1][j - 1]), a[j] + min(DP[i + 1][j - 1], DP[i][j - 2]));
        }
    }
    //return result
    return DP[0][n - 1];
}
int main()
{
    int n, item;
    cout << "Enter number of Coins\n";
    scanf("%d", &n);
    cout << "Enter coin values\n";
    vector<int> arr;
    for (int j = 0; j < n; j++) {
        scanf("%d", &item);
        arr.push_back(item);
    }

    cout << "Maximum possible winning is: " << MAX_WINNING(arr, n) << endl;

    return 0;
}

Output

 

Enter number of Coins
4
Enter coin values
10 30 5 8
Maximum possible winning is: 38

need an explanation for this answer? contact us directly to get an explanation for this answer

total answers (1)

This question belongs to these collections

Similar questions

need a help?

find thousands of online teachers now