Maximum Profit in Stock Buy and sell with at most K Transaction
In stock market, a person buys a stock and sells it on some future date. Given the stock prices of N days in form of an array Amount and a positive integer K, find out the maximum profit a person can make in at most K transactions. A transaction is buying the stock on some day and selling the stock at some other future day and new transaction can start only when the previous transaction has been completed.
Input:
K=3
N=7
Stock prices on N days:
10 25 38 40 45 5 58
Output:
88
Example:
Number of maximum transactions: 3
Total number of days, N: 7
To achieve maximum profit:
Stock bought at day1 (-10)
Stock sold at day5 (+45)
Stock bought at day6 (-5)
Stock sold at day7 (+58)
Total profit = 88
Total transactions made = 2
Explanation:
Let there are N number of days for transactions, say x1, x2, ..., xn
Now for any day xi
- Don't do any transaction on the day xi
- Transact on day xi, i.e., buy stock on some day xj and sell on day xi where j<i and i,j Є N
Total number of transactions can be made at most = K
Now we can formulate the maximum profit case using above two condition.
Let,
f(t,i)=maximum profit upto ith day and t transactions
Considering the above two facts about xi
f(t,i)=f(t,i-1) if there is no transaction made on day xi ...(1)
Max(f(t-1,j)+amount[i]-amount[j])
where j<i and i,j Є N if there is transaction on day xi ...(2)
Obviously, to maximize the profit we would take the maximum of (1) and (2)
Number of maximum transactions: 3
Total number of days, N: 7
Stock prices on the days are:
10 25 38 40 45 5 58
Below is a part of recursion tree which can show that how many overlapping sub problems there will be.
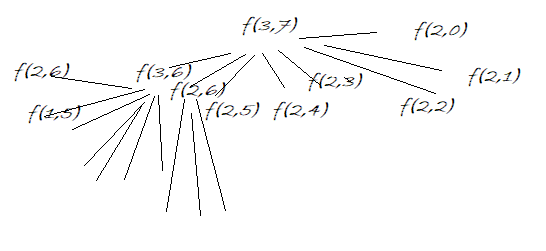
Figure 1: Partial recursion tree to show overlapping sub-problems
So we need dynamic programming...




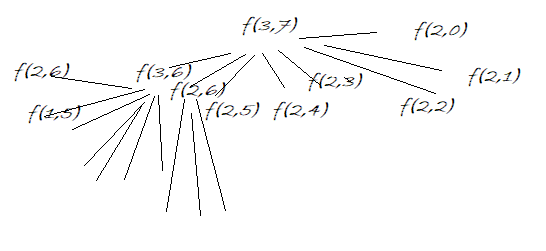
 C++ programming
C++ programming
Recursive Algorithm:
Function(t, i): //f(t, i) If i=0 f(t, i)=0 If t=0 f(t, i)=0 f(t, i)= f(t, i-1); //no transaction on day xi For j =0: i Find max(f(t-1,j) + amount(i)- amount(j) End For If the maximum found > f(t, i) update f(t, i) End IF Return f(t, i)Conversion to DP
For tabulation we need a 2D array, DP[k+1][n] to store f(t,i) Base case, for i 0 to k, DP[i][0]=0 //no profit on 0th day for i 0 to n-1, DP[0][j]=0 //no profit on 0 transaction To fill the higher values, for t=1 to k for i =1 to n-1 DP[t][i]=DP[t][i-1] for j= 0 to i-1 //buying on jth day and selling on ith day DP[t][i]=max(DP[t][i],DP[t-1][j]+ amount[i] –amount[j]) End for End for End for Result would be f(k,n) that is value of DP[k][n-1]Initial DP table
Try yourself to compute the DP table manually following the above algorithm and find out the result. Take some small example if necessary.
C++ implementation:
Output
need an explanation for this answer? contact us directly to get an explanation for this answer