Friends pairing problem
There are N friends, each one of them can remain single or can be paired up with some other friend. Each friend can be paired only once. Find out the total number of ways to do so. Since inputs are big return answer MOD 10^9+7.
Input:
Test case t
t no of lines with value of N
e.g.
3
5
4
1<=t<=100
1<=N<=100
Output:
t number of lines
Example:
Input: t=3, n=3
Output: 4
Input: n=4
Output: 10
Input: n=5
Output: 26
Explanation with example:
Let there are N number of friends, say x1, x2, ..., xn
Now, possible orderings can be:
- All are single. {x1, x2, ... , xn}
- x1 is single , others are paired contiguously(if n is odd). {x1, (x2, x3), ...}
So on. So if we try to figure out a formula then to observe that.
For any xi
- xi can be kept single
- xi can be paired with any other xj provided i≠j
Let f(n)= number of ways to pair for input N
Considering the above two facts about xi
If xn is kept single then f(n) = f(n-1) (same as number of ways excluding xn)
If xn is paired with any other friend then f(n)=(n-1)*f(n-2) (number of ways xn can be paired * sub-problem excluding xn and the paired one with it)
So the recursion function to solve the problem:
f(n)=f(n-1)+(n-1)*f(n-2)
For n=4
Friends are {1, 2, 3, 4}
So the pairings can be are:
{1, 2, 3, 4}
{1, 2, (3, 4)}
{1, (2, 3), 4}
{(1, 4), 2, 3}
{(1, 3), 2, 4}
{(2, 4), 1, 3}
{(1, 2), 3, 4}
{(1, 2), (3, 4)}
{(1, 3), (2, 4)}
{(1, 4), (2, 3)}
So total 10 possible type of pairings, hence output is 10
So the recursion tree for the above would be:
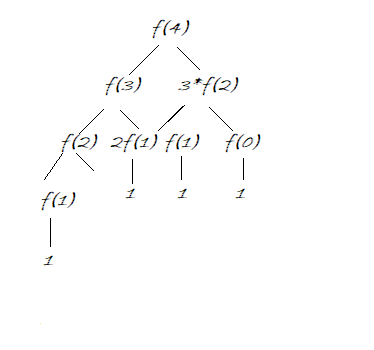
We see that we are evaluating many sub-problem several times. Like f(2) has been evaluated more than one time and the same also for others. It’s easily understandable that for such small input there are so many repeated computations, then for higher inputs, how many overlapping there will be. Here comes the need for DP, where we can use tabulation to solve bigger subproblems using smaller ones.




 C++ programming
C++ programming
Recursive Algorithm:
Function(n): If n==0 or n==1 Return 1 Else Return Function(n-1)+(n-1)*Function(n-2);Conversion to DP:
For tabulation we need arr[n+1] to store arr[0]=1 arr[1]=1 To fill the higher values, for i=2 to n arr[i]=arr[i-1]+(i-1)*arr[i+1] End forTo avoid Time Limit Exceed:
Since there are multiple test cases, we may get TLE even after using DP. To avoid that best way is to pre-compute the table up to input constraint. According to our example,
So better pre-compute arr[101] and return O(1) in time executing the test case query. No need to construct the table again and again for each test case.
C++ implementation:
Output
need an explanation for this answer? contact us directly to get an explanation for this answer