Minimum distance between two given nodes of a Binary Tree
Given a binary tree, and two node values your task is to find the minimum distance between them.
Node values are unique.
Example:
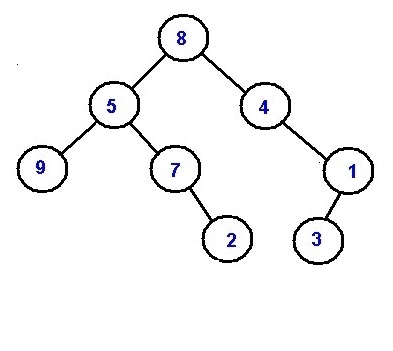
Let the two nodes to be 9 and 2, their min distance is 3, In case of 4 and 3 their min distance is 2.
One naïve idea can be searching for either of the nodes using BFS. Once either of the nodes is found, corresponding node is marked. We start searching for the other node incrementing distance. But one problem is result always is not guaranteed to be minimum.
Rather what actually should come to your mind is what can be closest node for both the target nodes (distance between those nodes that are to be found). The answer will be lowest common ancestor. So, we actually need to find the lowest common ancestor of two target nodes. Then, we can think the LCA to be root and the target nodes exist in two different branches. (Example 1)
Or there can be situation that both the target nodes exists on same root to leaf path that means one of the two target nodes itself is LCA. (Example 2)
However rest of our job is two find distance of respective target nodes from the LCA.
Let the distances to be distance1 and distance2 respectively.
Then the minimum distance between the two target nodes will be = distance1+distance2
How to find LCA?
Can be done using preorder traversal.
Pre-requisite:
Tree root, target node data values a, b
FUNCTION LCA (root, a, b) //base case IF(!root) return NULL; IF(root->data==a || root->data==b) //it ensures to root to be LCA return root; Node* l=findlowestancestor(root->left,a,b); Node* r=findlowestancestor(root->right,a,b); if(l && r) //this can only happen incase of LCA be root return root; return (l==NULL ?r:l); //NOT NULL one between l and r which contains LCA node END FUNCTIONAfter finding the LCA we compute the distance separately for two nodes. This can be done by level order traversal finding number of levels between target node and root (LCA).
Example with explanation:
Example 1:
Target nodes: 9 and 2 LCA: Node with value 5 Distance1: //distance between 5 and 9 1 Distance2: //distance between 5 and 2 2 Their min distance is 1+2=3Example 2:
Target nodes: 4 and 3 LCA: Node with value 4 (first target node itself) Distance1: //distance between 4 and 4 0 Distance2: //distance between 4 and 3 2 Their min distance is 0+2=2C++ implementation:
Output
need an explanation for this answer? contact us directly to get an explanation for this answer