Print All Nodes that don't have Sibling
Given a Binary Tree write a program to print the nodes which don’t have a sibling node. Print all the nodes separated by space which don't have sibling in the tree in sorted order if every node has a tree than print -1.
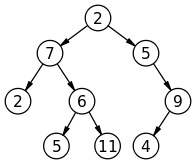
Explanation with example:
What is having sibling in tree?
A child node is said to have a sibling if the other node has the same parent as the child node. That means the nodes are siblings if they have same parent.
Like in the above example ‘2’ & ‘6’ are siblings as they have the same parent ‘7’.
In the above example the nodes that don’t have siblings are: 9, 4
Thus output:
4, 9 (sorted)
N.B: Root is not considered for sibling checking.
So, clearly a child node don’t have sibling, if its parent has only one pointer, either left or the right (that’s the child of course). Then we simply store the child node value & produce a sorted list to print. The traversal method we use here is level order traversal.
Algorithm:
1. Define tree Node structure 2. FUNCTION printSibling (Node* root) a) Declare a queue& a vector using STL Queue<Node*>q; vector<int>store; b) push the root EnQueue(q,root); Node* temp; While(queue is not empty) //do the level order traversal & check for siblings temp=DeQueue(q); //if the current node has only one child, definitely the child //has no sibling, thus store the child node value //left child pointer in NULL, right is not If temp->left==NULL&&temp->right!=NULL Addtemp->right node value in store; END IF //right child pointer in NULL, left is not If temp->left!=NULL&&temp->right==NULL Add temp->left node value in store; END IF // do level order traversing IF(temp->right) EnQueue(q, temp->right); IF(temp->left) EnQueue(q, temp->left); END WHILE c) If no node found without having sibling then vector size is zero then print -1 d) Elsesort the vector to print sorted node value END FUNCTIONC++ implementation to Print All Nodes that don't have Sibling
Output
need an explanation for this answer? contact us directly to get an explanation for this answer