Write a NumPy program to calculate the QR decomposition of a given matrix

Write a NumPy program to calculate the QR decomposition of a given matrix.

From Wikipedia: In linear algebra, a QR decomposition (also called a QR factorization) of a matrix is a decomposition of a matrix A into a product A = QR of an orthogonal matrix Q and an upper triangular matrix R. QR decomposition is often used to solve the linear least squares problem and is the basis for a particular eigenvalue algorithm, the QR algorithm.

Square matrix
Any real square matrix A may be decomposed as


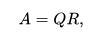
where Q is an orthogonal matrix (its columns are orthogonal unit vectors meaning {\displaystyle Q^{\textsf {T}}Q=QQ^{\textsf {T}}=I} {\displaystyle Q^{\textsf {T}}Q=QQ^{\textsf {T}}=I}) and R is an upper triangular matrix (also called right triangular matrix). If A is invertible, then the factorization is unique if we require the diagonal elements of R to be positive.
If instead A is a complex square matrix, then there is a decomposition A = QR where Q is a unitary matrix (so {\displaystyle Q^{*}Q=QQ^{*}=I} {\displaystyle Q^{*}Q=QQ^{*}=I}).
If A has n linearly independent columns, then the first n columns of Q form an orthonormal basis for the column space of A. More generally, the first k columns of Q form an orthonormal basis for the span of the first k columns of A for any 1 ≤ k ≤ n.[1] The fact that any column k of A only depends on the first k columns of Q is responsible for the triangular form of R.[1]