Write a menu-driven program to investigate the constant π. Model it after the program that explores the constant e. Pi (π) is the ratio of a circle’s circumference to its diameter. Many mathematicians have found ways to approximate π. For example, Machin’s formula is:
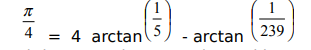
Leibniz found that π can be approximated by:
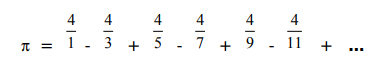
This is called a sum of a series. There are six terms shown in this
series. The first term is 4, the second term is –4/3, the third term is
4/5, and so forth. For example, the menu-driven program might have
the following options:
Print the result from Machin’s formula.
Print the approximation using Leibniz’ formula, allowing the user to
specify how many terms to use.
Print the approximation using Leibniz’ formula, looping until a “good”
approximation is found.
Exit the program.




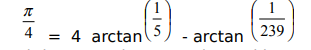
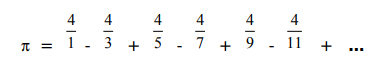
 Matlab
Matlab
Ch6Ex28.m
% This script explores pi
% Call a function to display a menu and get a choice
choice = pioption;
% Choice 4 is to exit the program
while choice ~= 4
switch choice
case 1
% Print result from Machin's formula
pimachin
case 2
% Approximate pi using Leibniz,
% allowing user to specify # of terms
pileibnizn
case 3
% Approximate pi using Leibniz,
% until a "good" approximation is found
pileibnizgood
end
% Display menu again and get user's choice
choice = pioption;
end
pioption.m
function choice = pioption
% Print the menu of options and error-check
% until the user pushes one of the buttons
% Format of call: pioption or pioption()
% Returns integer of user's choice, 1-4
choice = menu('Choose a pi option', 'Machin', ...
'Leibniz w/ n', 'Leibniz good', 'Exit Program');
% If the user closes the menu box rather than
% pushing one of the buttons, choice will be 0
while choice == 0
disp('Error - please choose one of the options.')
choice = menu('Choose a pi option', 'Machin', ...
'Leibniz w/ n', 'Leibniz good', 'Exit Program');
end
end
pimachin.m
function pimachin
% Approximates pi using Machin's formula and prints it
% Format of call: pimachin or pimachin()
% Does not return any values
machinform = 4 * atan(1/5) - atan(1/239);
fprintf('Using the MATLAB constant, pi = %.6f\n', pi)
fprintf('Using Machin''s formula, pi = %.6f\n',4*machinform)
end
pileibnizn.m
function pileibnizn
% Approximates and prints pi using Leibniz' formula
% Prompt user for number of terms n
% Format of call: pileibnizn or pileibnizn()
% Does not return any values
fprintf('Approximate pi using Leibiz'' formula\n')
% Call a subfunction to prompt user for n
n = askforn;
approxpi = 0;
denom = -1;
termsign = -1;
for i = 1:n
denom = denom + 2;
termsign = -termsign;
approxpi = approxpi + termsign * (4/denom);
end
fprintf('An approximation of pi with n = %d is %.2f\n', ...
n, approxpi)
end
function outn = askforn
% This function prompts the user for n
% It error-checks to make sure n is a positive integer
% Format of call: askforn or askforn()
% Returns positive integer n
inputnum = input('Enter a positive integer for n: ');
num2 = int32(inputnum);
while num2 ~= inputnum | num2 < 0
inputnum = input('Invalid! Enter a positive integer: ');
num2 = int32(inputnum);
end
outn = inputnum;
end
need an explanation for this answer? contact us directly to get an explanation for this answer