Many mathematical models in engineering use the exponential function. The general form of the exponential decay function is:
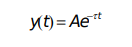
where A is the initial value at t=0, and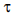 
is the time constant for the function. Write a script to study the effect of the time constant. To simplify the equation, set A equal to 1. Prompt the user for two different values for the time constant, and for beginning and ending values for the range of a t vector. Then, calculate two different y vectors using the above equation and the two time constants, and graph both exponential functions on the same graph within the range the user specified. Use a function to calculate y. Make one plot red. Be sure to label the graph and both axes. What happens to the decay rate as the time constant gets larger?
Matlab
Ch3Ex35.m
A = 1;
tau1 = input('Enter a time constant: ');
tau2 = input('Enter another time constant: ');
tstart = input('Enter the beginning t: ');
tend = input('Enter the end of t: ');
t = linspace(tstart,tend);
y1 = expfn(A, t, tau1);
y2 = expfn(A, t, tau2);
plot(t,y1,'r*',t,y2,'go')
xlabel('x')
ylabel('y')
title('Exp function')
legend('tau1','tau2')
expfn.m
function y = expfn(A,t,tau)
y = A * exp(-tau*t);
end
need an explanation for this answer? contact us directly to get an explanation for this answer