(Find a minimum spanning tree) Write a program that reads a connected graph from a file and displays its minimum spanning tree. The first line in the file contains a number that indicates the number of vertices (n). The vertices are labeled as 0, 1, ..., n-1. Each subsequent line describes the edges in the form of u1, v1, w1 | u2, v2, w2 | .... Each triplet in this form describes an edge and its weight. Figure 29.24 shows an example of the file for the corresponding graph. Note that we assume the graph is undirected. If the graph has an edge (u, v), it also has an edge (v, u). Only one edge is represented in the file. When you construct a graph, both edges need to be added.
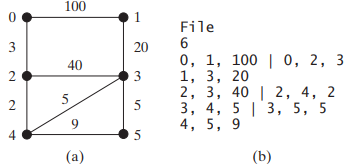
FIGURE 29.24 The vertices and edges of a weighted graph can be stored in a file
Your program should prompt the user to enter the name of the file, read data from the file, create an instance g of WeightedGraph, invoke g.printWeightedEdges() to display all edges, invoke getMinimumSpanningTree() to obtain an instance tree of WeightedGraph.MST, invoke tree.getTotalWeight() to display the weight of the minimum spanning tree, and invoke tree.printTree() to display the tree. Here is a sample run of the program:
Enter a file name: c:\exercise\WeightedGraphSample.txt
The number of vertices is 6
Vertex 0: (0, 2, 3) (0, 1, 100)
Vertex 1: (1, 3, 20) (1, 0, 100)
Vertex 2: (2, 4, 2) (2, 3, 40) (2, 0, 3)
Vertex 3: (3, 4, 5) (3, 5, 5) (3, 1, 20) (3, 2, 40)
Vertex 4: (4, 2, 2) (4, 3, 5) (4, 5, 9)
Vertex 5: (5, 3, 5) (5, 4, 9)
Total weight in MST is 35
Root is: 0
Edges: (3, 1) (0, 2) (4, 3) (2, 4) (3, 5)
(Hint: Use new WeightedGraph(list, numberOfVertices) to create a graph, where list contains a list of WeightedEdge objects. Use new WeightedEdge(u, v, w) to create an edge. Read the first line to get the number of vertices. Read each subsequent line into a string s and use s.split("[\\|]") to extract the triplets. For each triplet, use triplet.split("[,]") to extract vertices and weight.)





 Java programming
Java programming