(Algebra: 2 × 2 linear equations) Design a class named LinearEquation for a 2 × 2 system of linear equations:
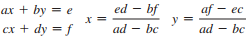
The class contains:
■ Private data fields a, b, c, d, e, and f.
■ A constructor with the arguments for a, b, c, d, e, and f.
■ Six getter methods for a, b, c, d, e, and f.
■ A method named isSolvable() that returns true if ad - bc is not 0.
■ Methods getX() and getY() that return the solution for the equation.
Draw the UML diagram for the class and then implement the class. Write a test program that prompts the user to enter a, b, c, d, e, and f and displays the result. If ad - bc is 0, report that “The equation has no solution.” See Programming Exercise 3.3 for sample runs.




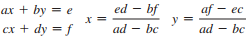
 Java programming
Java programming
LinearEquation.java
need an explanation for this answer? contact us directly to get an explanation for this answer