The Hamiltonian of a gas of photons within an empty cavity of volume V is given by the expression
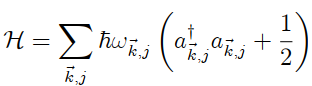
where j = 1, 2 indicates the polarization, k is the wave vector,
w→k,j = ck,
c is the velocity of light, and k = |k| .
(a) Use the formalism of the occupation numbers (second quantization) to obtain the canonical partition function asso- ciated with this system.
(b) Show that the internal energy is given by
U = σV T n.
Obtain the value of the constants n and σ.
(c) Consider the Sun as a black body at temperature T≈5800 K. The solar diameter and the distance between the Sun and the Earth are of the order of 109 m and 1011 m, respec- tively. Obtain the intensity of the total radiation that reaches the surface of Earth. What is the value of the pressure of this radiation?
The canonical partition function is given by
In order to calculate the internal energy we write
where the first term in the right-hand-side leads to well-known (divergent) energy of the quantum vacuum. If we measure the internal energy with respect to the vacuum, we have
In d dimensions, it is easy to check that this internal energy with respect to the quantum vacuum is given by
U = σV T n,
where n = d + 1 (n = 4 in three dimension, according to the Stefan-Boltzmann law) and
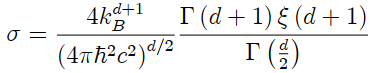
need an explanation for this answer? contact us directly to get an explanation for this answer