Consider again the gas of N ultrarelativistic free electrons, within a container of volume V ,
belongs to book: Introduction to statistical physics|sílvio-r.-a.-salinas|| Chapter number:9| Question number:9
All Answers
total answers (1)
belongs to book: Introduction to statistical physics|sílvio-r.-a.-salinas|| Chapter number:9| Question number:9
total answers (1)
The grand partition functions may be written as
ln Ξ = ln Ξ+ + lnΞ-
with
We then write
with
where
As the Fermi energy is the chemical potential at zero tempera- ture, we have
from which we obtain
For µBH << xT (H = 0), we have
The magnetization is given by
M = µB (N+ - N—) ,
which leads to
so that we have the zero-field susceptibility
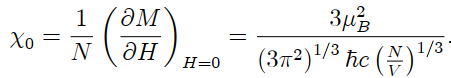
need an explanation for this answer? contact us directly to get an explanation for this answer