Show that the chemical potential of an ideal classical gas of N monatomic particles, in a container of volume V , at temperature T , may be written as
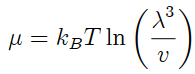
where v = V/N is the volume per particle, and
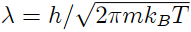
is the thermal wavelength. Sketch a graph of µ/kBT versus T . Obtain the first quantum correction to this result. That is, show that the chemical potential of the ideal quantum gas may be written as the expansion
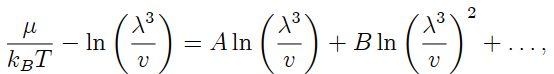
and obtain explicit expressions for the prefactor A for fermions and bosons. Sketch a graph of µ/kBT versus λ-2 (that is, versus the temperature in convenient units) for fermions, bosons, and classical particles.




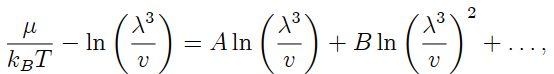
 Physics
Physics
The grand partition function of the ideal quantum gas is given by
We now write an expansion in terms of powers of x,
The first term corresponds to the classical limit (there is no difference between fermions and bosons).
The second term gives the first quantum correction. In the thermodynamic limit, we have
The classical limit is given by
from which we have
Thus,
which leads to the well-known result
with
Check that the same result can be obtained in the classical for- malism of the grand ensemble,
with the introduction of the ”cor- rect Boltzmann counting”, N!, and of the ”quantum dimensional correction" of the classical phase space, k3N .
The first quantum correction of this result is given by
Thus,
which can be written as
Taking into account that x << 1, which means that λ3v << 1, we can write
and
from which we have
Therefore,
which leads to the expression
Try to use the same scheme to show that B = -1/16 (check that B assumes the same value for either fermions or bosons).
need an explanation for this answer? contact us directly to get an explanation for this answer