An ideal gas of N atoms of mass m is confined to a vessel of volume V , at a given temperature T. Calculate the classical limit of the chemical potential of this gas. Now consider a ”two-dimensional” gas of NA free particles adsorbed on a surface of area A. The energy of an adsorbed particle is given by
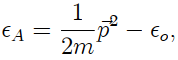
where pp is the (two-dimensional) momentum, and xo > 0 is the binding energy that keeps the particle stuck to the surface. In the classical limit, calculate the chemical potential µA of the adsorbed gas.
The condition of equilibrium between the adsorbed particles and the particles of the three-dimensional gas can be expressed in terms of the respective chemical potentials. Use this condition to find the surface density of adsorbed particles as a function of temperature and pressure p of the surrounding gas.
In the thermodynamic limit, the chemical potential of the three-dimensional gas is given by
For the adsorbed gas, we have the classical limit
which yields the chemical potential
From the physical requirement of equilibrium, µ = µA, we obtain NA/A in terms of temperature and pressure.
need an explanation for this answer? contact us directly to get an explanation for this answer