Consider a classical gas of N weakly interacting molecules, at temperature T ,

Consider a classical gas of N weakly interacting molecules, at temperature T ,in an applied electric field E→ . Since there is no permanent electric dipole moment, the polarization of this system comes from the induction by the field. We then suppose that the Hamiltonian of each molecule will be given by the sum of a standard translational term plus an ”internal term.” This internal term involves an isotropic elastic energy, which tends to preserve the shape of the molecule, and a term of interaction with the electric field. The configurational part of the internal Hamiltonian is be given by

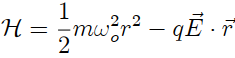
Obtain the polarization per molecule as a function of field and temperature. Obtain the electric susceptibility. Compare with the results of the last problem. Make some comments about the main differences between these results. Do you know any physical examples corresponding to these models?