Consider again the preceding problem. The canonical par- tition function can be written as an integral form,
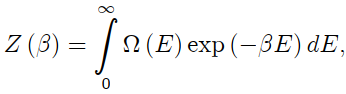
where Ω(E) is the number of accessible microscopic states of the system with energy E. Note that, in the expressions for Z (β) and Ω(E), we are omitting the dependence on the number N of oscillators. Using the expression for Z (β) obtained in the last exercise, perform a reverse Laplace transformation to obtain an asymptotic form (in the thermodynamic limit) for Ω(E). Compare with the expression calculated in the framework of the microcanonical ensemble.




 Physics
Physics
First, we use an integral representation of the 6-function (see Appendix) to write
Inserting the result of the previous exercise, we have
which can be written in the form of a saddle-point integration (see Appendix),
where u = E/N. Using the asymptotic integration techniques of the Appendix, we locate the saddle point at β = 1/u and write the asymptotic form (for N → ∞),
Therefore, we have the entropy per oscillator,
which should be compared with the well-known result for the classical one-dimensional harmonic oscillator in the microcanon- ical ensemble.
need an explanation for this answer? contact us directly to get an explanation for this answer